یکی از دلایلی که بیت کوین برای مبتدیان میتواند سردرگم کننده باشد این است که فناوری بیت کوین از مفهوم مالکیت، تعریف جدیدی ارائه میدهد.
به طور سنتی مالک چیزی نظیر خانه یا مقداری پول بودن یعنی اینکه که تصدی آن را در اختیار دارد یا تصدی آن را به نهاد مورد اعتماد نظیر بانک واگذار کرده است.
در مورد بیت کوین شرایط متفاوت است. بیت کوین به صورت مرکزی یا محلی ذخیره نمیشود و بدین ترتیب هیچ نهادی تصدی آن را به عهده ندارد. بیت کوین به عنوان سوابق در دفتر کل توزیع شده ای به اسم بلاک چین وجود دارند. نسخه های یکسانی از این دفترکل توزیع شده توسط شبکه ای از رایانه های به هم متصل به اشتراک گذاشته میشود. داشتن بیت کوین به معنای داشتن قابلیت انتقال دادن کنترل آن به فرد دیگر است. این امر با ایجاد سابقه انتقال در بلاک چین امکان پذیر است. اما چه چیزی باعث به وجود آمدن این قابلیت میشود؟ جواب این سوال دسترسی آن جفت کلید عمومی و خصوصی ECDSA میباشد. این پاسخ به چه معناست و چگونه بیت کوین را ایمن میکند؟
با هم نگاهی دقیق تر به این موضوع می اندازیم.
الگوریتم ECDSA مخفف عبارت Elliptic Curve Digital Signature Algorithm و به معنای الگوریتم امضای دیجیتال مبتنی بر منحنی بیضوی است. ECDSA فرآیندی است که از منحنی بیضوی و میدان متناهی برای امضای اطلاعات استفاده میکند. امضای اطلاعات در این الگوریتم به شیوه ای انجام میشود که اشخاص ثالث میتوانند اعتبار امضا را تایید کنند در حالی که فقط امضا کننده قابلیت ایجاد امضا را در اختیار دارد. در خصوص بیت کوین، اطلاعات امضا شده همان تراکنشی است که مالکیت را انتقال میدهد.
الگوریتم ECDSA، رویه های امضا و تایید تفکیک شده دارد. هر رویه یک الگوریتم شامل چند عملیات محاسباتی است. الگوریتم امضا و فرآیند تایید به ترتیب از کلید خصوصی و کلید عمومی استفاده میکنند. در ادامه این مقاله، مثالی در این خصوص بیان خواهیم کرد.
اما ابتدا به توضیح منحنی های بیضوی و میدان های متناهی میپردازیم.
منحنی های بیضوی
منحنی بیضوی به صورت جبری طبق فرمول زیر بیان میشود:
y2 = x3 + ax + b
اگر a برابر با صفر و b برابر با ۷ باشد (نسخه مورد استفاده توسط بیت کوین) سهمی به شکل زیر خواهد بود:
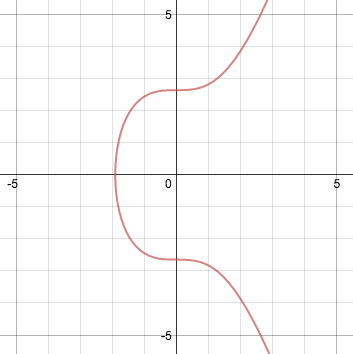
منحنی های بیضوی ویژگی های مفیدی دارند. برای مثال، خط غیر عمودی که دو نقطه غیر مماس در منحنی را قطع میکند همواره از روی نقطه سوم بر روی منحنی عبور میکند. ویژگی دیگر این است که خط غیر عمودی مماس با منحنی در یک نقطه، دقیقا یک نقطه دیگر بر روی منحنی را قطع میکند.
با استفاده از این ویژگی ها میتوانیم دو عملیات دیگر را نیز تعریف کنیم: افزودن نقطه و دو برابر کردن مختصات نقطه
افزودن نقطه با فرمول P + Q = R به صورت دستیابی به مختصات محور x نقطه تلاقی سوم R بر روی خطی است که شامل P و Q است. درک این تعریف با شکل زیر آسانتر میشود:
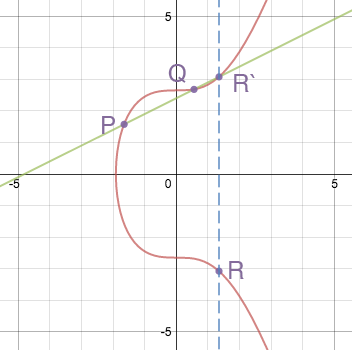
دو برابر کردن مختصات نقطه هم با فرمول P + P = R و با یافتن خط مماس با نقطه ای که قرار است مختصاتش دو برابر شود و به دست آوردن مختصات محور x نقطه قطع کننده R میباشد. در ادامه به مثالی در این خصوص میپردازیم:
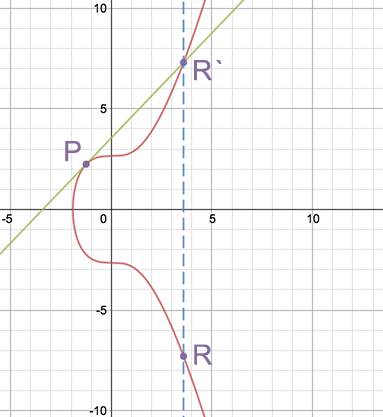
این دو عملیات با یکدیگر برای ضرب اسکالر با فرمول R = a P و جمع نقطه P با خودش به تعداد a بار میباشد. برای مثال داریم:
R = 7P
R = P + (P + (P + (P + (P + (P + P)))))
فرآیند ضرب اسکالر معمولا با استفاده از ترکیب عملیات افزودن نقطه و دو برابر کردن مختصات نقطه، ساده تر میشود. برای مثال داریم:
R = 7P
R = P + 6P
R = P + 2 (3P)
R = P + 2 (P + 2P)
در اینجا، 7P به دو مرحله دو برابر کردن مختصات نقطه و دو مرحله افزودن نقطه تقسیم شده است.
میدان های متناهی
میدان متناهی در بافت ECDSA را میتوان به صورت طیف از پیش تعیین شده ای از اعداد مثبت در نظر گرفت که در این طیف هر محاسبهای قابل انجام است. هر عددی خارج از این محدوده گرد میشود و داخل طیف قرار میگیرد.
ساده ترین روش برای بیان این مورد، محاسبه باقی مانده هاست که توسط اپراتور ماژول ها (mod) بیان میشود. برای مثال داریم:
9 mod 7 = 2
در اینجا میدان متناهی، ماژول ۷ است و حاصل تمام عملیات mod در این میدان در طیف صفر الی ۶ قرار میگیرد.
ساماندهی کردن
الگوریتم ECDSA از منحنی های بیضوی در بافت میدان متناهی استفاده میکند که ظاهر آن را به شدت تغییر میدهد اما در فرمول ها و ویژگی های خاص آن تغییری ایجاد نمیکند. فرمول مشابه شکل فوق در میدان متناهی ماژول ۶۷ به صورت زیر میباشد:
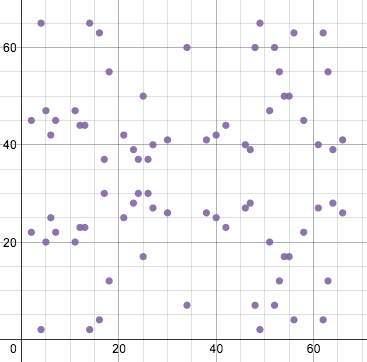
اکنون مجموعه ای از نقاط داریم که تمام مقادیر x و y اعداد صحیح بین صفر الی ۶۶ میباشند. به خاطر داشته باشید که منحنی هم چنان تقارن افقی خود را حفظ میکند.
افزودن نقطه و دو برابر کردن مختصات نقطه از نظر ظاهری مقداری با یکدیگر فرق دارند. خطوط این گراف در جهت های عمودی و افقی قرار میگیرند. بنابراین افزودن نقاط (2, 22) و (6, 25) به صورت شکل زیر خواهد بود:
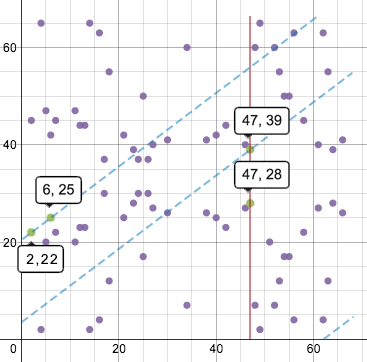
نقطه تلاقی سوم (47, 39) و نقطه بازتاب (47, 28) میباشد.
الگوریتم ECDSA و بیت کوین
پروتکلی نظیر بیت کوین، مجموعه ای از پارامترها را برای منحنی بیضوی و میدان متناهی خود انتخاب میکند که برای تمام کاربران پروتکل ثابت میباشد. این پارامترها شامل فرمول استفاده شده، ماژول اصلی میدان و نقطه پایه ای است که بر روی منحنی قرار میگیرد. ترتیب نقطه پایه ای که به صورت مستقل انتخاب نمیشود و تابعی از پارامترهای دیگر است را از نظر تصویری میتوان به عنوان تعداد دفعاتی در نظر گرفت که نقطه میتواند به مختصات خودش اضافه شود تا شیب به بی نهایت برسد.
بیت کوین از اعداد بسیار بزرگی برای نقطه پایه ای، ماژول اصلی و ترتیب خود استفاده میکند. در واقع تمام کاربردهای عملی از ECDSA از مقادیر بسیار بزرگ استفاده میکنند. امنیت الگوریتم به بزرگ بودن این مقادیر بستگی دارند، در نتیجه حملات بروت فورس و مهندسی معکوس غیرممکن میشود.
در مورد بیت کوین شرایط زیر برقرار است:
معادله منحنی بیضوی:
y2 = x3 + 7
ماژول اصلی:
2256 – 232 – 29 – 28 – 27 – 26 – 24 – 1 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
نقطه پایه ای:
04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
ترتیب:
FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
چه کسی و چرا این اعداد را انتخاب کرده است؟ تحقیقات و تمهیدات بسیار زیادی در خصوص انتخاب پارامترهای مناسب صورت گرفته است. علیرغم این موارد، به نظر میرسد که عدد تصادفی بسیار بزرگی ممکن است روش بکدور ساخت مجدد کلید خصوصی را پنهان کرده باشد. به طور خلاصه میتوان گفت این تعریف خاص به اسم secp256k1 بوده و بخشی از خانواده راهکارهای منحنی بیضوی در میدان های متناهی مورد استفاده در رمزنگاری است.
کلیدهای خصوصی و کلیدهای عمومی
با کنار گذاشتن این تشریفات، اکنون در موقعیتی قرار داریم که میتوانیم کلیدهای خصوصی و عمومی و نحوه ارتباط آن ها را متوجه شویم. به صورت خلاصه میتوان گفت: در ECDSA، کلید خصوصی عدد انتخابی غیرقابل پیش بینی بین ۱ الی سفارش میباشد. کلید عمومی از کلید خصوصی و ضرب اسکالر نقطه پایه ای به تعداد مقدار کلید خصوصی حاصل میشود. این تعریف را به صورت فرمول میتوان اینگونه بیان کرد:
کلید عمومی= کلید خصوصی * نقطه پایه ای
این فرمول نشان میدهد که حداکثر تعداد کلیدهای خصوصی برابر با سفارش است.
در میدان ممتد میتوانیم خط مماس را رسم کنیم و کلید عمومی را بر روی گراف قرار دهیم، اما فرمول هایی وجود دارد که در بافت میدان های متناهی به همین نتیجه دست مییابند. افزودن نقطه p+q برای یافتن r به صورت زیر تعریف میشود:
c = (qy – py) / (qx – px)
rx = c2 – px – qx
ry = c (px – rx) – py
و دو برابر کردن نقطه p برای یافتن r نیز به صورت زیر است:
c = (3px2 + a) / 2py
rx = c2 – 2px
ry = c (px – rx) – py
در عمل، محاسبه کلید عمومی به عملیات دو برابر کردن نقطه و افزودن نقطه تقسیم میشود.
مثال زیر را با اعداد کوچک بیان میکنیم تا مفهوم مناسبی از نحوه ساخت کلیدها و استفاده از آنها در امضا و تایید ارائه شود. پارامترهای مورد استفاده عبارتند از:
فرمول:
y2 = x3 + 7
ماژول اصلی: ۶۷
نقطه پایه ای: (2, 22)
ترتیب: ۷۹
کلید خصوصی: ۲
ابتدا به یافتن کلید عمومی میپردازیم. از آنجایی که ساده ترین کلید خصوصی ممکن با مقدار ۲ را انتخاب کرده ایم، فقط به یکبار دو برابر کردن مختصات نقطه از نقطه پایه ای نیاز داریم. محاسبات این عملیات به شرح زیر می باشد:
c = (3 * 22 + 0) / (2 * 22) mod 67
c = (3 * 4) / (44) mod 67
c = 12 / 44 mod 67
در اینجا سوال دیگری بیان میکنیم: در بافت میدان متناهی که نتیجه باید همواره عدد صحیح باشد، چگونه دست بندی انجام میشود؟ ما باید عملیات ضرب معکوس را انجام بدهیم که از حوصله این مقاله خارج است. اما به محاسبات زیر میتوانید اعتماد کنید:
44-1 = 32
سپس در ادامه داریم:
c = 12 * 32 mod 67
c = 384 mod 67
c = 49
rx = (492 – 2 * 2) mod 67
rx = (2401 – 4) mod 67
rx = 2397 mod 67
rx = 52
ry = (49 * (2 – 52) – 22) mod 67
ry = (49 * (-50) – 22) mod 67
ry = (-2450 – 22) mod 67
ry = -2472 mod 67
ry = 7
بنابراین کلید عمومی ما متناظر با نقطه (52, 7) است. تمام این اقدامات برای کلید خصوصی ۲ میباشد.
این عملیات یعنی دریافت کلید عمومی از کلید خصوصی، در مقایسه با معکوس این اقدام یعنی دریافت کلید خصوصی از کلید عمومی از نظر محاسباتی آسان تر است زیرا این اقدام اگرچه از نظر تئوری امکان پذیر است اما به دلیل پارامترهای بزرگ به کار رفته در رمزنگاری بیضوی، از نظر محاسباتی اجرا شدنی نیست. بنابراین مسیر کلید خصوصی به کلید عمومی به صورت یک طرفه طراحی شده است.
همانند کلید خصوصی، کلید عمومی نیز معمولا با رشته هگزادسیمال بیان میشود. اما چگونه از روی نقطه ای بر روی صفحه که با دو عدد بیان میشود، چگونه میتوان به یک عدد دست یافت؟ در کلید عمومی فشرده نشده، دو عدد ۲۵۶ بیتی که بیانگر مختصات x و y میباشند در یک رشته بلند به یکدیگر چسبیده اند. هم چنین میتوانیم از تقارن منحنی بیضوی برای تولید کلید عمومی فشرده بهره ببریم. این امر با حفظ مقدار x و توجه به اینکه نقطه بر روی کدام نیمه منحنی قرار دارد انجام میشود. یا توجه به این اطلاعات جزیی، میتوانیم هر دو مختصات را بازیابی کنیم.
امضای اطلاعات با کلید خصوصی
اکنون که کلید خصوصی و کلید عمومی را در اختیار داریم، اطلاعات را امضا میکنیم.
اطلاعات میتواند به هر اندازه ای وجود داشته باشد. قدم اول معمولا، هش کردن اطلاعات برای تولید عددی است که میزان بیت یکسان (۲۵۶ بیت) داشته باشد. در اینجا به منظور ساده سازی، از مراحل هش کردن میگذریم و فقط اطلاعات خام z را امضا میکنیم. در ادامه به نقطه پایه G، ترتیب n و کلید خصوصی d میگوییم. دستور العمل امضا به شرح زیر است:
عدد صحیحی بین ۱ و n-۱ انتخاب کنید.
نقطه (x, y) را به صورت زیر با استفاده از ضرب اسکالر محاسبه کنید:
(x, y) = k * G
مقدار r را با فرمول زیر به دست آورید. اگر r=۰ باشد آنگاه به مرحله اول برمیگردیم:
r = x mod n
مقدار s را با فرمول زیر به دست آورید. اگر s=۰ باشد آنگاه به مرحله اول برمیگردیم:
s = (z + r * d) / k mod n
امضا به صورت (r, s) به دست میآید.
یادآور میشویم که در مرحله چهارم، اگر جواب ها به صورت اعشاری باشند، صورت باید در معکوس مخرج ضرب شود. در مرحله اول، این نکته مهم است که k در امضاهای مختلف تکرار نشده باشد و این امر توسط شخص ثالث قابل حدس نیست. بدین ترتیب، k باید تصادفی باشد یا توسط ابزارهای تعیین کننده ای که از اشخاص ثالث پنهان شده است تولید شود. در غیر این صورت، استخراج کلید خصوصی از مرحله۴ امکان پذیر میشود زیرا s، z، k و n مشخص میباشند.
فرض میکنیم که داده ما دارای عدد ۱۷ باشد. متغیرهای ما به شکل زیر خواهند بود:
z= ۱۷ (داده)
(ترتیب) n = ۷۹
(نقطه پایه) (G = (2, 22
d = ۲ (کلید خصوصی)
انتخاب عدد تصادفی نیز به شرح زیر است:
عدد k = عدد صحیحی بین ۱ الی n-۱
عدد k = ۳ (برای سادهتر شدن مثال، این عدد را انتخاب کردیم)
نقطه را محاسبه کنید. این امر به همان روش تعیین کلید عمومی انجام میشود با این تفاوت که به منظور خلاصه کردن این عملیات، محاسبات را برای افزودن نقطه و دوبرابر کردن مختصات آن حذف کرده ایم:
(x, y) = 3G
(x, y) = G + 2G
(x, y) = (2, 22) + (52, 7)
(x, y) = (62, 63)
x = 62
y = 63
r یافتن
r = x mod n
r = 62 mod 79
r = 62
s یافتن
s = (z + r * d) / k mod n
s = (17 + 62 * 2) / 3 mod 79
s = (17 + 124) / 3 mod 79
s = 141 / 3 mod 79
s = 47 mod 79
s = 47
توجه داشته باشید که در مثال فوق، میتوانیم اعداد را بر ۳ تقسیم کنیم زیرا جواب ها اعداد صحیح بودند. در موارد واقعی، از معکوس k استفاده میکنیم که خواهیم داشت:
s = (z + r * d) / k mod n
s = (17 + 62 * 2) / 3 mod 79
s = (17 + 124) / 3 mod 79
s = 141 / 3 mod 79
s = 141 * 3-1 mod 79
s = 141 * 53 mod 79
s = 7473 mod 79
s = 47
امضای ما در حالت (r, s) = (62, 47)
همانند کلید عمومی و کلید خصوصی، این امضا نیز معمولا توسط رشته هگزادسیمال بیان میشود.
تایید امضا با استفاده از کلید عمومی
اکنون چندین داده و امضا برای داده مورد نظر داریم. شخص ثالثی که کلید عمومی داشته باشد میتواند اطلاعات و امضا را دریافت کند و تایید کند که ما ارسال کننده هستیم. در ادامه به نحوه کار این مورد میپردازیم.
در این مثال Q را کلید عمومی در نظر میگیریم و سایر متغیرات در مراحل تایید امضت به شرح زیر میباشند:
- تایید مقدار r و s بین ۱ الی n-۱
- w = s-1 mod n
- u = z * w mod n
- v = r * w mod n
- x, y) = uG + vQ) نقطه
تایید r = x mod n. در غیر این صورت امضا نامعتبر است
چرا این مراحل درست میباشند؟ ما از مرحله اثبات میگذریم. در این خصوص، از دستورالعمل زیر پیروی کنید. بار دیگر متغیرات ما به شرح زیر است:
z = 17
(r, s) = (62, 47)
n = 79
G = (2, 22)
Q = (52, 7)
تایید مقدار r و s بین ۱ الی n-۱
r: 1 <= 62 < 79
s: 1 <= 47 < 79
محاسبه w:
w = s-1 mod n
w = 47-1 mod 79
w = 37
محاسبه u:
u = zw mod n
u = 17 * 37 mod 79
u = 629 mod 79
u = 76
محاسبه v:
v = rw mod n
v = 62 * 37 mod 79
v = 2294 mod 79
v = 3
محاسبه نقطه (x, y):
(x, y) = uG + vQ
دو برابر کردن مختصات نقطه و افزودن نقطه را در uG و vQ به طور جداگانه محاسبه میکنیم.
uG = 76G
uG = 2(38G)
uG = 2( 2(19G) )
uG = 2( 2(G + 18G) )
uG = 2( 2(G + 2(9G) ) )
uG = 2( 2(G + 2(G + 8G) ) )
uG = 2( 2(G + 2(G + 2(4G) ) ) )
uG = 2( 2(G + 2(G + 2( 2(2G) ) ) ) )
برای راحتی کار، ۷۵ عملیات افزودن متوالی را به ۶ عملیات افزودن نقطه و دو برابر کردن مختصات نقطه کاهش میدهیم. هنگامی که اعداد بسیار بزرگ باشند این امر بسیار کارآمد است.
در نتیجه، عملیات را از آخر به اول بیان میکنیم:
uG = 2( 2(G + 2(G + 2( 2( 2(2, 22) ) ) ) ) )
uG = 2( 2(G + 2(G + 2( 2(52, 7) ) ) ) )
uG = 2( 2(G + 2(G + 2(25, 17) ) ) )
uG = 2( 2(G + 2( (2, 22) + (21, 42) ) ) )
uG = 2( 2(G + 2(13, 44) ) )
uG = 2( 2( (2, 22) + (66, 26) ) )
uG = 2( 2(38, 26) )
uG = 2(27, 40)
uG = (62, 4)
اکنون برای vQ داریم:
vQ = 3Q
vQ = Q + 2Q
vQ = Q + 2(52, 7)
vQ = (52, 7) + (25, 17)
vQ = (11, 20)
با کنار هم قرار دادن این موارد خواهیم داشت:
(x, y) = uG + vQ
(x, y) = (62, 4) + (11, 20)
(x, y) = (62, 63)
مشخصا مرحله پنجم، قسمت عمده ای از عملیات را به خود اختصاص میدهد. در مرحله آخر داریم:
تایید r = x mod n
r = x mod n
62 = 62 mod 79
62 = 62
اکنون امضای ما معتبر است.
نتیجه گیری
ما در این مقاله به توضیح رابطه پیچیده ریاضیاتی بین کلید عمومی و کلید خصوصی پرداختیم. هم چنین مشاهده کردیم که چطور حتی در ساده ترین مثال ها نیز، اصول ریاضیاتی امضاها و تایید به چه سرعتی پیچیده میشوند. این پیچیدگی بسیار زیاد را هنگامی که پارامترهای حاضر، اعداد ۲۵۶ بیتی میباشند میپذیریم. ما در این مقاله مشاهده کردیم که کاربرد هوشمندانه ساده ترین رویه های ریاضیاتی میتواند مسیر یکطرفه ضروری برای حفظ عدم تقارن اطلاعات ایجاد کند که مالکیت بیت کوین را تعریف میکند. هم چنین به اعتماد مجددی به استحکام این سیستم دست یافتیم که شامل محافظت کاملا ایمن از کلیدهای خصوصی ما میباشد.
به عبارت دیگر به این دلیل است که میگویند بیت کوین با علم ریاضیات پشتیبانی میشود. اگر به مسائل پیچیده کدنویسی علاقه دارید امیدواریم که این مقاله به شما کمک کند تا قدم بعدی را در بحث مورد نظر بردارید.













