نسبت شارپ چیست؟ کاربرد انواع نسبت شارپ و فرمول محاسبه برای سرمایه گذاری

نسبت شارپ (Sharp Ratio) توسط “ویلیام اف. شارپ (William F. Sharpe)” به منظور کمک به سرمایه گذاران برای درک بهتر “سود یک سرمایه گذاری نسبت به ریسک آن” توسعه یافته است. ویلیام شارپ برای این قضیه موفق به دریافت جایزه نوبل شد.

این نسبت، میانگین سود دریافتی و نرخ بهره بدون ریسک، به ازای هر واحد از نوسان کلِ بازار است.

تفاضلِ نرخ بهره بدون ریسک و میانگین سود دریافتی، به سرمایه گذار اجازه می‌دهد تا تفکیک بهتری از نسبت سود به زیان داشته باشد. در اصل، هرچقدر که مقدار نسبت شارپ بالاتر باشد، سود تعدیل شده بر اساس ریسک نیز بیشتر خواهد شد.

فرمول و محاسبه نسبت شارپ

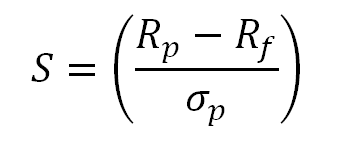
• R_P= سود سبد سهام
• R_F= نرخ بهره بدون ریسک
• _و σp​= تغییرات احتمالی سودِ مازاد سبد سهام

نسبت شارپ بر اساس نرخ بهره بدون ریسک منهای سود سبد سهام، تقسیم بر تغییرات احتمالی سودِ مازاد سبد سهام محاسبه می‌شود.

رمزگشایی نسبت شارپ

نسبت شارپ به یکی از مهم ترین و گسترده ترین روش ها برای محاسبه سود تعدیل شده بر اساس ریسک بدل شده است.

تئوری “دارایی مدرن” یا (MPT) می‌گوید که افزودن سرمایه به منظور سرمایه گذاری در سبدی از سهام هایی که همبستگی ندارند، می‌تواند مجموع ریسک را بدون از دست دادن اصل سود کاهش دهد. این افزایش تنوع ممکن است نسبت شارپ این نوع سبدها را به نسبت سایر سبدهایی که دارای همبستگی بیشتری هستند، افزایش دهد.

برای این که این نسبت افزایش یابد، سرمایه گذاران باید در نظر بگیرند که ریسک مساوی با نوسانی است که بی دلیل اتفاق افتاده است؛ اما این نوسان ممکن است به حدی محدود باشد که در تمامی معاملات اتفاق نیافتد.

نسبت شارپ می‌تواند در محاسبه رفتارهای گذشته سبدها نیز استفاده شود. به این صورت که به جای گذاشتن اعداد کنونی و واقعی در فرمول، سرمایه گذاران اعداد سبدهای گذشته را در فرمول قرار می‌دهند و به این ترتیب نسبت شارپ آن را محاسبه می‌کنند.

نسبت شارپ همچنین می‌تواند مشخص کند که سود یک سبد سهامی بر اساس سرمایه گذاری هوشمند بوده است یا یک سرمایه گذاری با ریسک فراوان. همچنین یک سبد یا صندوق سرمایه گذاری می‌تواند سودی بیشتر از حد مورد انتظار به ارمغان بیاورد. تنها در صورتی می‌توان آن را یک سرمایه گذاری موجه تلقی کرد، که سود آن بر پایه ریسک بیش از حد نباشد.

هرچه نسبت شارپ یک سبد سهام بزرگتر باشد، عملکرد سود تعدیل شده بر اساس ریسک آن بهتر خواهد بود. اگر نتایج تحلیل نسبت شارپ عددی منفی نشان دهد، به این معناست که نرخ بهره بدون ریسک آن بزرگ تر از سود آن سبد سهامی است و انتظار می‌رود که بازدهی سبد نیز منفی شود. در هر یک از این موارد، نسبت شارپ منفی نتیجه مثمر ثمری به ما ارائه نخواهد داد.

نسبت شارپ در مقابل نسبت سورتینو

یکی از شاخه های نسبت شارپ، نسبت سورتینو (Sortino Ratio) است، که اثرات حرکت صعودی قیمت بر روی انحراف عادی را حذف می‌کند تا با این کار، تمرکز را بر روی توزیع سودی ببرد که قبل از رسیدن به آن هدف قیمتی انتظار آن را داریم.

همچنین نسبت سورتینو، سود مورد نظر را به جای نرخ بهره بدون ریسک در صورت کسر فرمول جایگزین می‌کند. پس فرمول نسبت سورتینو به این صورت است:

• سود سبد سهام – سود مورد انتظار تقسیم بر سود مورد انتظار

یکی دیگر از شاخه های نسبت شارپ، نسبت ترینور (Treynor Ratio) است، که از ثبات بازار و یا وابستگی بین بازار و سبد سهام انتخابی استفاده می‌کند. هدف نسبت ترینور خنثی کردن ریسک اضافی سرمایه گذار نسبت به ریسک ذاتی بازار است. به عبارتی دیگر، نسبت ترینور به سرمایه گذار کمک می‌کند تا مازاد بر ریسک ذاتی بازار، خطر نکند. فرمول نسبت ترینور به شرح زیر است:

• سود سبد سهام – نرخ بهره بدون ریسک تقسیم بر عدد ثبات بازار

محدودیت های نسبت شارپ

 

نسبت شارپ از انحراف عادیِ سود به عنوان میانگین کل ریسک در مخرج فرمول استفاده می‌کند، که این نشان دهنده توزیع نرمال سود است.

به هر حال سودها در بازارهای اقتصادی، با میانگین آن اختلاف دارند؛ چراکه یک مبلغ بزرگ می‌تواند روند نزولی بازار را تغییر دهد و یا باعث نوسانات شدید شود. معمولاً در حالت عادی بازار، حرکت قیمت در هر یک از دو جهت صعودی و نزولی به یک اندازه ریسکی است.

نسبت شارپ می‌تواند به دارندگان سبد سهام کمک کند تا تاریخچه سود تعدیل شده بر اساس ریسک آنها به دست آید. این می‌تواند با طولانی تر کردن تایم فریم یا بازه زمانی اندازه گیری شود و در محاسبه نوسانات قیمت دچار اشتباه کمتری شود.

برای مثال اگر عدد انحراف عادی در چارت روزانه را صفر در نظر بگیریم، عددی که در پاسخ به دست می‌آوریم بزرگ تر از عددی است که در پاسخ به همین فرمول در چارت هفتگی به دست می‌آوریم. و به همین ترتیب نیز نتیجه چارت هفتگی، بزرگ تر از نتیجه نمودار ماهیانه خواهد شد.

انتخاب یک تایم فریم (Timeframe) یا بازه زمانی نسبت به تایم فریم قبلی برای به دست آوردن بهترین نسبت شارپ، یکی دیگر از راه هایی است که می‌توان اطلاعاتی که باعث مخدوش شدن سود تعدیل شده بر اساس ریسک می‌شوند را شناسایی کرد.

یک نمونه از کاربرد نسبت شارپ

نسبت شارپ اغلب برای مقایسه کلی تغییرات ریسک – سود برای مواقعی که یک سهام جدید وارد سبد شما می‌شود کاربرد دارد.

برای مثال، یک سرمایه گذار می‌خواهد یک سهام قرارداد آتی مثل بکت (Bakkt) را به سبد خود اضافه کند. این سبد دارای تعدادی سهام و اوراق قرضه است که در سال گذشته ۱۵% سود به او رسانده است. نرخ بهره بدون ریسک کنونی ۳.۵% ، و نوسان سود این سبد نیز ۱۲% است؛ که نتیجه نسبت شارپ آن ۹۵.۸% خواهد شد:

• ۳.۵% – ۱۵% تقسیم بر ۱۲% = ۹۵.۸%

سرمایه گذار معتقد است که افزودن قراردادهای آتی به سبد سهام، سود معامله در سال حاضر را به ۱۱% کاهش می‌دهد؛ اما نرخ نوسان سود را نیز از ۱۲% به ۷% کاهش می‌دهد. با این حال نرخ بهره بدون ریسک ثابت است.

این سرمایه گذار از همین فرمول می‌تواند برای محاسبه سود سال آینده استفاده کنند. به این ترتیب که ۱۱% سود معامله امسال را منهای ۳.۵% نرخ بهره بدون ریسک می‌کند و سپس آن را تقسیم بر ۷% نرخ نوسان سود می‌کند:

• ۳.۵%-۱۱% تقسیم بر ۷% = ۱۰۷%

با این فرمول می‌توان نشان داد که هرچند سهام معاملات آتی سود سبد سهام را کاهش می‌دهد، اما از طرف دیگر بر روی ریسک موجود نیز تأثیر فراوان می‌گذارد. در نتیجه با کاهش ریسک، می‌توان سود را افزایش داد.

اگر در صورت افزودن سهام آتی جدید نسبت شارپ کاهش یابد، این سهام نباید به سبد اضافه شود.

این مثال به خوبی توضیح می‌دهد که عملکرد نسبت شارپ بر اساس نوسانات گذشته بازار، می‌تواند آینده بازار را پیش بینی کند.

در آخر

• نسبت شارپ می‌تواند با استفاده از نوسانات گذشته، حرکات آینده بازار را پیش بینی کند و همچنین ریسک آن را نیز بسنجد.
• مقدار بالای نسبت شارپ در یک سبد سهام، در مقایسه با مقدار پایین این نسبت در سبد سهام مشابه، بهتر است.
• نقطه ضعف نسبت شارپ این است که سود سرمایه گذاری باید به شکل مستقل توزیع شود.