کریپتو با ویتالیک؛ بررسی زوج‌‌ سازی منحنی بیضوی

ویتالیک بوترین یکی از مغزهای متفکر پایه‌گذار شبکه اتریوم در کنار گوین وود و چارلز هاسکینسون است. این نابغه روس یکی از مهم‌ترین افراد فعال در حوزه بلاکچین است. از این رو در مجموعه میهن بلاکچین تصمیم گرفتیم تا مطالب بلاگ شخصی او که به نوعی تاریخ زنده بلاکچین است را برای علاقمندان ترجمه کنیم. مطلبی که در ادامه می‌آید ترجمه‌ای از مطلبی به همین نام در سایت بوترین است که در تاریخ ۱۴ ژانویه ۲۰۱۷ منتشر شد. با این مطلب خواندنی همراه باشید.

پیش از هر چیز اخطار دهم که مطلب پیش رو شامل مباحث ریاضی است:

یکی از فروض کلیدی زمینه‌ساز برخی از کاربردهای مهم رمزنگاری همچون امضاهای آستانه‌ای قطعی (deterministic threshold signatures)، zk-SNARKها و دیگر فرم‌های ساده‌تر اثبات‌های بی‌نیاز به دانش منحنی‌های بیضوی، زوج سازی منحنی‌ بیضوی است. زوج‌های منحنی بیضوی (elliptic curve pairings) یا نگاشت‌های دوخطی (bilinear maps) به تازگی به تاریخ سی ساله استفاده از خم‌های بیضوی در رمزنگاری و تولید امضاهای دیجیتال اضافه شده‌اند؛ این زوج‌ها شکلی از «ضرب رمزنگاری‌شده – encrypted multiplication» را به وجود می‌آورند که وسعت عمل پروتکل‌های مبتنی بر منحنی‌های بیضوی می‌افزاید. هدف از مقاله بررسی زوج‌ سازی منحنی‌ بیضوی و چگونگی اصول کار آن‌هاست.

انتظار نمی‌رود که دفعه اولی که این مطلب را مطالعه می‌کنید چیزی از آن متوجه شوید یا حتی دفعه دهمی که آن را می‌خوانید؛ چرا که این مطالب واقعا دشوار هستند. اما امید این است که این مطلب به شما ایده‌ای کلی در خصوص نحوه کار این ابزارها دهد.

مبحث منحنی‌های بیضوی مبحثی غیربدیهی و مشکل است و تلقی این مقاله بر این است که شما می‌دانید آن‌ها چگونه کار می‌کنند؛ در صورتی که این موضوع را نمی‌دانید، خواندن این مطلب را به شما پیشنهاد می‌کنم.

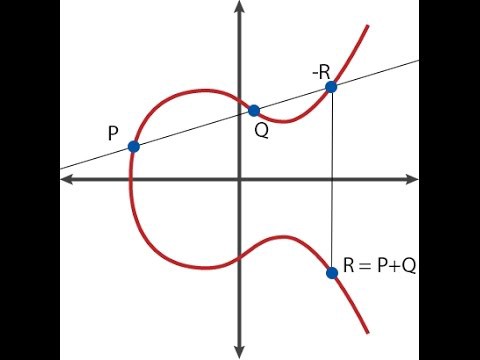
به عنوان خلاصه‌ای کوتاه، رمزنگاری منحنی بیضوی شامل اشیا ریاضیاتی به نام نقاط (نقاطی دو بعدی با مختصات x و y) با فرمول‌هایی ویژه برای جمع و تفریق آن‌هاست (برای محاسبه مختصات R = P + Q) همچنین می‌توانید یک نقطه را در عددی صحیح ضرب کنید (برای مثال P ⋅ n = P + P + . . . + P اگرچه راهی سریع‌تر برای محاسبه وجود دارد به خصوص اگر n بزرگ باشد).

نقطه‌ای ویژه به نام «نقطه در بی‌نهایت (O)» وجود دارد که معادل صفر در حساب عادی است بدین ترتیب که P+O = P. همچنین هر منحنی مرتبه‌ای دارد که عددی است که به ازای آن و برای هر P، P ⋅ n = O است (n مرتبه منحنی است) و به همین ترتیب P ⋅ ( n + 1 ) = P , P ⋅ ( 7 ⋅ n + 5 ) = P ⋅ 5

همچنین نقطه‌ای به نام «نقطه مولد – G» وجود دارد که مشابه عدد یک عمل می‌کند. به شکل نظری، هر نقطه‌ای به جز O می تواند یک نقطه G باشد. تنها چیزی که اهمیت دارد این است که G استانداردسازی شود.

زوج‌ها می‌توانند آزادی عمل بیشتری در چک کردن برخی اعمال و معادلات پیچیده‌تر در فضای نقاط منحنی‌های بیضوی به شما دهند – برای مثال اگر P = G ⋅ p , Q = G ⋅ q و R = G ⋅ r شما می‌توانید با داشتن P، Q و R به عنوان ورودی، صحت p ⋅ q = r را بررسی کنید. این مساله شاید باعث شود که گمان کنید شکسته شدن منحنی‌های بیضوی تضمینی است چرا که با دانستن P می‌توان اطلاعاتی از p به دست آورد اما مشخص شده است که نشت اطلاعات به شدت کنترل شده است. به طور مشخص مساله تصمیم دیفای – هلمن آسان است اما محاسبات مساله دیفی – هلمن (در مثال بالا معادل است با اینکه با دانستن P و کیو، R = G ⋅ p ⋅ q را محاسبه کنیم) و مساله لگاریتم گسسته (استخراج p از P) از لحاظ محاسباتی ناممکن است (حداقل اگر تا پیش از این نیز چنین بوده است).

سومین راه نگاه به زوج‌ سازی منحنی بیضوی که بیش از هر راه دیگری روشنگر استفاده‌های مدنظر ماست، این است که به نقاط منحنی بیضوی به چشم اعداد یک طرفه رمزنگاری شده (رمزنگاری(p) = p.G = P) بنگرید و در حالی که ریاضیات سنتی منحنی‌های بیضوی به شما اجازه می‌دهد تا محدودیت‌های خطی را بر روی اعداد (برای مثال اگر P = G.p و Q = G.q و R = G.r باشد، آن گاه چک کردن 5 ⋅ P + 7 ⋅ Q = 11 ⋅ R عملا چک کردن 5 ⋅ p + 7 ⋅ q = 11 ⋅ r است) بررسی کنید، زوج‌ها به شما اجازه می‌دهند تا محدودیت‌های درجه دوم (برای مثال e ( P , Q ) ⋅ e ( G , G ⋅ 5 ) = 1 همانند چک کردن p ⋅ q + 5 = 0 است) را بررسی کنید. بررسی معادلات درجه دوم برای ما کافی است تا بتوانیم با امضاهای آستانه‌ای قطعی، برنامه‌های حسابی درجه دوم و تمام این موارد مدنظرمان کار کنیم.

حال، این عملگر خنده‌دار e ( P , Q ) که در بالا معرفی کردیم چیست؟ این زوج است. ریاضی‌دانان برخی اوقات آن را نگاشت دوخطی می‌نامند؛ واژه دو خطی بدین معناست که دو شروط دو معادله زیر را ارضا می‌کند:

توجه داشته باشید که دو عملگر . و + می‌توانند دلخواهد باشند؛ وقتی به دنبال خلق موجودیت‌های جدید ریاضی هستید، مادامی که عملگرها در راه‌های رایج ثبات داشته باشند (برای مثال a + b = b + a , ( a ⋅ b ) ⋅ c = a ⋅ ( b ⋅ c ) و ( a ⋅ c ) + ( b ⋅ c ) = ( a + b ) ⋅ c)، از نظر علم جبر اهمیتی ندارد که چگونه تعریف می شوند.

اگر P، Q و S اعداد ساده باشند، آن‌گاه ساختن یک یک زوج ساده، آسان خواهد بود: می‌توانیم … تعریف کنیم. سپس خواهیم داشت:

و می‌بینید که دوخطی است!

اما چنین زوج‌های ساده‌ای برای رمزنگاری مناسب نیستند چرا که با موجودیت‌هایی سر و کار دارند که اعداد صحیح هستند و تحلیل آن‌ها آسان است. اعداد صحیح اعمال ریاضی همچون تقسیم، گرفتن لگاریتم و دیگر محاسبات را ساده می‌کنند و خبری از مفاهیمی همچون کلید عمومی و تابع یک طرفه نیست. همچنین زوجی که در بالا معرفی شد را می‌توان به راحتی شکاند – با دانستن x و e(x,y) می‌توانید با محاسبه تقسیم و لگاریتم به y برسید. در حالی که ما می‌خواهیم که شی ریاضیاتی مدنظر ما تا حد امکان به جعبه سیاه نزدیک باشد؛ به نحوی که بتوانید جمع کنید، تفریق کنید، ضرب کنید یا تقسیم کنید اما هیچ کار دیگری نتوانید انجام دهید. این جا جایی است که منحنی‌های بیضوی و زوج‌ سازی منحنی بیضوی به میان می‌آیند.

ثابت شده است که می‌توان بر روی نقاط منحنی بیضوی نگاشت دوخطی گرفت – یعنی تابعی همچون e ( P , Q ) تعریف کرد که ورودی P و Q آن نقاط منحنی بیضوی باشند و خروجی چیزی باشد که آن را المان (F_p)^{12} می‌نامیم (جزییات بیشتر به نوع منحنی بستگی دارد اما در اینجا صرفا به این المان خاص خواهیم پرداخت) اما ریاضیات مربوط به آن بسیار سنگین است.

در ابتدا بگذارید میدان اول (هیات اول) و میدان توسیع (extension field) را توضیح دهم. شاید منحنی بیضوی زیبایی که در تصویر ابتدایی پست دیدید به نظر برسد که با استفاده از اعداد حقیقی عادی ساخته شده است اما اگر از اعداد حقیقی عادی در رمزنگاری استفاده کنیم، می‌توان از لگاریتم‌ها برای شکستن آن استفاده کرد و همه‌چیز فرو می‌پاشد. همچنین فضای ذخیره‌سازی لازم برای ذخیره و نشان دادن اعداد به شدت زیاد می‌شود. در نتیجه از اعداد در میادین اول (prime field) استفاده می‌کنیم.

میدان اول از مجموعه‌ای از اعداد ۰، ۱، ۲… p-1 تشکیل شده است که در آن عدد p، عددی اول است و اعمال مختلف ریاضی به شکل زیر تعریف می‌شود:

در واقع تمامی اعمال با استفاده از پیمانه p صورت می‌گیرد (برای آشنایی با حساب پیمانه‌ای اینجا را ببینید). تقسیم موردی خاص است؛ به شکل عادی 3/2 یک عدد صحیح نیست و ما می‌خواهیم فقط با اعداد صحیح سر و کار داشته باشیم بنابراین باید سعی کنیم تا ایکسی را بیابیم که x ⋅ 2 = 3 و در اینجا . به ضرب پیمانه‌ای اشاره می‌کند که در بالا تعریف شد. با کمک قضیه کوچک فرما حقه‌ای که برای توان زدیم کار می‌کند اما راه سریع‌تری برای آن وجود دارد؛ با استفاده از الگوریتم تعمیم‌یافته اقلیدسی. فرض کنید که p = 7 است، حال به چند مثال زیر توجه کنید:

اگر با این نوع از ریاضیات به اندازه کافی کلنجار روید، متوجه خواهید شد که کاملا ثبات نتیجه دارد و تمامی قوانین رایج را برآورده می‌سازد. دو مثال آخر نشان می‌دهد که چگونه ( a / b ) ⋅ b = a؛ همچنین می‌توانید ببینید که ( a + b ) + c = a + ( b + c ) , ( a + b ) ⋅ c = a ⋅ c + b ⋅ c و تمام موارد جبری دیگری که در دبیرستان آموختید برقرار است. در دنیای واقعی، منحنی‌های بیضوی و نقاط و معادلات مربوط به آن معمولا در میادین اول محاسبه می‌شوند.

حال بیایید راجع به میدان توسیع صحبت کنیم. احتمالا تاکنون با چنین میدانی مواجه شده‌اید؛ رایج‌ترین مثالی که در کتب ریاضی با آن مواجه شده‌اید میدان اعداد مختلط است که به میدان اعداد حقیقی با المان اضافی \sqrt{-1} = i توسعه می‌یابد. به طور خلاصه میدان توسیع با فرض وجود یک میدان اولیه و افزودن المان جدید به آن و سپس تعریف روابط میان المان جدید و دیگر المان‌های موجود (مانند مثالی که در این جا آورده شده i ² + 1 = 0) تعریف می‌شود. همچنین لازم است که این معادله برای هیچ عددی که پیش‌تر در میدان اولیه موجود بوده است برقرار نباشد. در این میان مجموعه تمام ترکیبات خطی المان‌های میدان اولیه و المان‌های جدید نیز بررسی می‌شود.

توسیع میدان اول نیز ممکن است؛ برای مثال می‌توانیم میدان اول مود ۷ را که در بالا توصیف کردیم با i توسیع کنیم و آن‌گاه خواهیم داشت:

آخرین نتیجه ممکن است کمی گنگ به نظر رسد؛ اتفاقی که آن جا افتاد این بود که در ابتدا اجزای ضرب را به 4 i ⋅ 2 + 4 i ⋅ i شکستیم که برابر است با 8i – 4 و سپس از آن جا که در مود (پیمانه) ۷ اعمال ریاضی را انجام می‌دهیم خواهیم داشت i + 3 برای تقسیم چنین خواهیم کرد:

a / b : ( a ⋅ b ( p ^{2 − 2} ) ) % p

دقت کنید که حالا توان قضیه کوچک فرما به جای p، p به توان دو است که اگر بار دیگر بخواهیم بهینه‌تر عمل کنیم می‌توانیم از الگوریتم تعمیم‌یافته اقلیدس برای انجام این کار استفاده کنیم. برای هر ایکس این میدان، داریم x^{p^2 – 1} = 1 پس می‌توانیم p^2 – 1 را مرتبه گروه ضربی در میدان بنامیم.

قضیه اساسی جبر باعث می‌شود که در صورت توسیع درجه دوم اعداد حقیقی که آن را اعداد مختلط می‌نامیم، نتوانیم دیگر پیش بریم و آن را بیشتر توسعه دهیم چرا که هر رابطه ریاضی (یا حداقل جبری) که بتوانید بین المان جدید j و اعداد مختلط موجود بیان کنید، حداقل یک عدد مختلط دیگر وجود دارد که بتواند آن قاعده را برآورده سازد. در میادین اول این مشکل وجود ندارد و می‌توانیم پیش رویم و توسیع مکعبی (درجه سوم) (در این حالت روابط ریاضی بین المان جدید w و المان‌های میدان موجود رابطه‌ای درجه سه است بنابراین ۱، w و w^2 هر کدام به شکل خطی مستقل از دیگری هستند)، توسیع‌های مرتبه بالاتر، توسیع توسیع‌ها و غیره را بسازیم. بر روی چنین اعداد مختلط پیمانه‌ای است که زوج‌های منحنی بیضوی بنا می‌شوند.

برای کسانی که علاقه‌مند دانستن ریاضیات مربوطه به شکل کد هستند، بررسی ریپو زیر توصیه می‌شود:

Py Pairing

اکنون به زوج‌های منحنی بیضوی بازگردیم. یکی زوج منحنی بیضوی نگاشتی است که G 2 × G 1 → G t که:

• G₁ یک منحنی بیضوی است که نقاط آن معادله به فرم y^2 = x^3 + b برآورده می‌سازند و تمامی مختصات آن المان‌های F_p هستند (آن‌ها اعدادی ساده هستند تنها تفاوت این است که محاسبات به شکل پیمانه‌ای انجام می‌شود).
•  G₂ یک منحنی بیضوی است که نقاط آن معادله‌ای مشابه منحنی پیشین را برآورده می‌سازند. تفاوت در این است که مختصات نقاط المان‌هایی از (F_p)¹² هستند (آن‌ها اعدادی مشابه اعداد مختلطی هستند که در بالا تعریف کردیم؛ این عدد جادویی جدید w را به شکل چند جمله‌ای درجه دوازدهم تعریف می‌کنیم که فرمی به شکل w 12 − 18 ⋅ w 6 + 82 = 0 دارد).
• G_t نوعی شی ریاضی است که نتیجه منحنی‌های بیضوی را به دست می‌دهد. در مورد منحنی‌هایی که ما به آن علاقه‌مند هستیم، G_t به شکل (F_p)¹² است (همان اعدادی که در منحنی پیشین به کار رفت).

مهم‌ترین خصوصیتی که باید برآورده شود، دوخطی بودن است که در این مورد عبارتست از:

دو مولفه مهم دیگر موارد زیر هستند:

• بهینه بودن محاسبات
• ناتبهگونی

چگونه این کار را انجام دهیم؟

ریاضیات دخیل در این ماجرا مشکل و پیچیده‌تر از چیزی است که تا بدینجا مشاهده کردیم اما اصول کار را شرح خواهم داد. پیش از همه، احتیاج داریم تا مفهوم مقسوم علیه را تعریف کنیم که در واقع راهی برای نمایش توابع بر روی نقاط منحنی‌های بیضوی است. مقسوم علیه یک تابع صفرها و نقاط بی‌نهایت تابع را می‌شمرد. برای فهم اینکه این قضیه به چه شکل است، بیایید چند مثال ببینیم. نقطه فرضی P = ( P x , P y ) در نظر بگیرید. تابع زیر را تعریف می‌کنیم:

f ( x , y ) = x − P x

مقسوم علیه [ P ] + [ − P ] − 2 ⋅ [ O ] است (کروشه‌ها برای نمایش اینکه ما به نقطه P در مجموعه صفرها و بی‌نهایت‌های تابع اشاره داریم و نه خود نقطه P اشاره دارد؛ [ P ] + [ Q ] مشابه [ P + Q ] نیست). منطق این کار به شرح زیر است:

• تابع در P برابر با صفر است چرا که ایکس برابر است با P_x پس x − P x = 0

• تابع در P- صفر است پس P- و P دارای مختصات یکسان x هستند.
• تابع با میل x به بی‌نهایت به سمت بی‌نهایت میل می‌کند بنابراین می‌توانیم بگوییم که تابع در O برابر با بی‌نهایت است. دلیلی فنی وجود دارد که بی‌نهایت باید دوبار شمرده شود بنابراین O با ضریب ۲- اضافه می‌شود (منفی بودن آن بدین خاطر است که بی‌نهایت است و نه صفر).

دلیل فنی مذکور به شکل ساده این است: از آنجا که معادله خم به فرم x^3 = y^2 + b, y است، y یک و نیم بار سریع‌تر از x به سمت بی‌نهایت میل می‌کند. بنابراین اگر تابعی خطی داشته باشیم که تنها شامل x باشد، ضریب بینهایت باید دو بوده و اگر تنها شامل y است باید با ضریب ۳ بی‌نهایت همراه شود.

حال تابع خط را در نظر بگیرید:

ax + by + c = 0

که در آن ثوابت به نحوی انتخاب شده‌اند که خط از نقاط P و Q گذر کند. به خاطر نحوه کار عمل جمع منحنی‌های بیضوی این بدین معنی است که از نقطه P-Q- نیز می‌گذرد. از آن جا که میل به بی‌نهایت وابسته به ایکس و ایگرگ است، مقسوم علیه به شکل [ P ] + [ Q ] + [ − P − Q ] − 3 ⋅ [ O ] خواهد بود.

می‌دانیم که هر تابع گویا (تابعی که تنها با استفاده از تعداد متناهی از اعمال جمع، تفریق و تقسیم بر روی مختصات نقاط تعریف شده است) به شکل منحصر به فرد به مقسوم علیه پاسخ می‌دهد یعنی اگر دو تابع F و G مقسوم علیه یکسانی داشته باشند، آن‌گاه F = G.k که k عدد ثابتی است.

برای هر دو تابع F و G مقسوم علیه تابع F.G برابر است با مقسوم علیه تابع F به اضافه مقسوم علیه G؛ برای مثال اگر f ( x , y ) = P x − x آن گاه ( f 3 ) = 3 ⋅ [ P ] + 3 ⋅ [ − P ] − 6 ⋅ [ O ] نقاط P و منفی P سه بار شمرده می‌شوند تا جبران این حقیقت که تابع f³ به صفر سه بار سریع‌تر میل می‌کند را کنند.

قضیه‌ای وجود دارد که بیان می‌کند که اگر کروشه‌ها را از مقسوم علیه یک تابع حذف کنید، جمع نقاط باید O شوند. در دو مثال پیشین (O ( [ P ] + [ Q ] + [ − P − Q ] − 3 ⋅ [ O ] و P + Q − P − Q − 3 ⋅ O = O )) این قضیه به روشنی واضح است. همچنین این قضیه بیان می‌‌دارد که هر مقسوم علیه‌ای که این ویژگی را داشته باشد، مقسوم علیه تابع است.

حال آماده‌ایم که نگاهی به زوج‌ سازی تیت (Tate) بیاندازیم. توابع زیر را در نظر بگیرید که هر یک به وسیله مقسوم علیه‌هایشان تعریف شده‌اند:

حال نگاهی به حاصل ضرب F P ⋅ F Q ⋅ g n بیاندازید. مقسوم علیه عبارتست از:

n ⋅ [ P ] − n ⋅ [ O ] + n ⋅ [ Q ] − n ⋅ [ O ] + n ⋅ [ P + Q ] − n ⋅ [ P ] − n ⋅ [ Q ] + n ⋅ [ O ]

که به عبارت زیر ساده می‌شود:

n ⋅ [ P + Q ] − n ⋅ [ O ]

توجه کنید که شکل تابع دقیقا مشابه مقسوم علیه‌های F_P و F_Q بالاست بنابراین F P ⋅ F Q ⋅ g n = F P + Q

حالا فرایندی به نام به توان رساندن نهایی را انجام می‌دهیم. در این مرحله نتیجه توابع بالا را گرفته و آن را به توان z = (p^{12} – 1) / n می‌رسانیم که در آن p^{12} – 1 مرتبه گروه ضربی در (F_p)^{12} است (داریم x ∈ ( F p ) 12 , x ( p 12 − 1 ) = 1). اگر این مرحله را به هر جوابی که پیش از این به توان n رسیده باشد اعمال کنید، توان p^{12} – 1 نتیجه خواهد بود که همواره مساوی ۱ خواهد شد. بنابراین پس از مرحله به توان رساندن نهایی، g^n از بین می‌رود و خواهیم داشت: F P z ⋅ F Q z = ( F P + Q ) z

این دوخطی بودن را می‌رساند.

حال اگر بخواهیم تابعی داشته باشیم که در هر دو آرگومان دوخطی باشد باید از ریاضیات پیچیده‌تری استفاده کنید؛ به جای گرفتن مقداری از F_P به شکل مستقیم، باید F_P یک مقسوم علیه را بگیرید و اینجاست که زوج تیت کامل خودش را نشان می‌دهد. برای مطالعه بیشتر اینجا و اینجا را مشاهده کنید.

برای مشاهده بکارگیری عملی نسخه اصلاح شده زوج تیت که آن را زوج بهینه ایت (optimal Ate pairing) می‌نامیم، به این لینک بروید. در این کد از الگوریتم میلر استفاده شده است که برای محاسبه F_P لازم است.

ممکن بودن چنین زوج‌هایی مزایای و معایبی دارد؛ از سویی بدین معناست که می‌توانیم از تمام پروتکل‌هایی که بر پایه این زوج‌ها بنا شده‌اند استفاده کنیم اما معنی دیگر آن این است که باید در انتخاب منحنی بیضوی بیشتر دقت کنیم.

هر منحنی بیضوی شامل خصیصه‌ای به نام درجه نشاندن (embedding degree) است؛ کوچکترین k ای که p^k – 1 مضربی از n باشد (که p عدد اول استفاده شده برای میدان و n مرتبه خم است). در میادین بالا، k = 12 است و در میادین استفاده شده برای ECC سنتی (که در آن به زوج سازی اهمیتی نمی‌دهیم) درجه نشاندن اغلب بسیار بزرگ است تا جایی زوج سازی از لحاظ محاسباتی ناممکن است. اما اگر دقت نکنیم می‌توان میادین تولید کرد که k = 4 و یا حتی 1 باشد.

اگر k = 1 باشد، آنگاه مساله لگاریتم گسسته برای خم‌های بیضوی ( به شکل خلاصه شکستن رمزنگاری مبتنی بر این روش) را می‌توان به مساله ریاضی مشابه در P = G ⋅ p تقلیل داد که حل آن بسیار آسان‌تر خواهد بود (به این روش حمله MOV می‌گویند). استفاده از خم‌هایی ب ادرجه نشاندن ۱۲ یا بیشتر این تقلیل را ناممکن می سازد و یا حل مساله لگاریتم گسسته مرتبط آن قدر سخت خواهد بود که مشابه پیدا کردن کلید خصوصی از روی کلید عمومی به روش عادی باشد (که از لحاظ محاسباتی تقریبا ناممکن است).