ویتالیک بوترین، خالق اتریوم و یکی از چهرههای تاثیرگذار دنیای ارزهای دیجیتال است. بلاگ شخصی او، تاریخچهای از پیشرفتهای صورت گرفته در دنیای بلاک چین است. از این رو در میهن بلاکچین بر آن شدیم تا با ترجمه مطالب بوترین، خوانندگان محترم را با سیر پیشرفت تئوری این حوزه آشنا کنیم. مطلبی که در ادامه خواهید خواند، در ۹ نوامبر ۲۰۱۷ در وبسایت شخصی بوترین منتشر شده است. ویتالیک در این مطلب، شرحی بر نحوه کار ZK-STARKها که در آن زمان در ابتدای راه خود بودند، ارائه میدهد. برای آشنایی با مفاهیم اشاره شده در این مطلب، نوشتههای زیر میتواند راهگشا باشد:
ZK-STARK چیست و چه تفاوتی با ZK-SNARK دارد؟
امیدوارم که افراد بیشتری حالا با ZK-SNARKها آشنا شده باشند؛ تکنولوژی همهمنظوره و موجز بینیاز به دانشی که میتواند برای انواع و اقسام کاربردها، از محاسبات قابل تایید گرفته تا پرایوسی کوینها به کار رود. چیزی که ممکن است از آن اطلاع نداشته باشید، عموزاده این فناوری است: ZK-STARK. حرف T در این کلمه مخفف کلمه شفاف (Transparent) است. این فانوری یکی از ضعفهای اساسی اسنارکها را برطرف کرده است. ضعفی که مربوط به «راهاندازی اولیه نیازمند اعتماد – Trusted Setup» این تکنولوژی است. همچنین استارکها فروض رمزنگاری بسیار سادهتری دارند که نیاز به منحنیهای بیضوی، زوجسازی و فرض دانش توان (Knowledge of Exponent) را برطرف میکند و در عوض تنها بر هشها و نظریه اطلاعات استوار است. به طور خلاصه این بدین معنی است که این روش حتی در برابر پردازش کوانتومی نیز مقاوم است.
اما این مزایا بیهزینه نیست: حجم گواه از ۲۸۸ بایت به چندصد کیلوبایت افزایش پیدا میکند. برخی اوقات این هزینه مازاد ارزشش را ندارد اما در برخی دیگر از مواقع، به خصوص در مورد بلاک چینهای عمومی که نیاز به حداقلسازی اعتماد بالاست، ارزشش را خواهد داشت. به ویژه اگر زمانی سازوکار منحنیهای بیضوی روزی بشکند یا کامپیوترهای کوانتومی به حقیقت بپیوندند.
نحوه ساخت گواه ZK-STARK
با بیان این مقدمه، حال بررسی کنیم که این نوع دیگر از گواه بینیاز به دانش چگونه کار میکند؛ ابتدا بیایید مرور کنیم که یک گواه بینیاز از دانش همهمنظوره موجز چگونه کار میکند. فرض کنید که تابعی عمومی به نام f، ورودی خصوصی x و ورودی عمومی y را داریم. میخواهید ثابت کنید که x را میدانید به نحوی که f(x) = y، بی آن که مقدار x را افشا کنید.علاوه بر آن، برای این که گواه شما موجز باشد، باید آن را به نحوی قابل تایید و صحتسنجی کنید که انجام این عمل کوتاهتر از محاسبه f به طول انجامد.
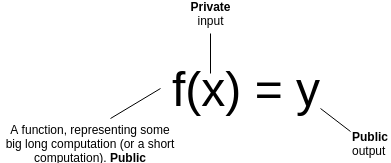
بیایید چند مثال را مرور کنیم:
- f محاسباتی است که انجام در کامپیوتر خانگی حدود دو هفته طول میکشد اما میتوان آن را به کمک دیتا سنترها طی دو ساعت انجام داد. شما محاسبات (کد اجرای f) را برای دیتا سنتر میفرستید، دیتا سنتر آن را اجرا میکند و نتیجه (y) را به همراه گواه به شما بازمیگرداند. شما نتیجه را تنها در عرض چند میلیثانیه صحتسنجی میکنید و اطمینان حاصل میکنید که به راستی y جواب درست است.
- شما تراکنش رمزشدهای به فرم «X1 موجودی سابق من، X2 موجودی سابق شما، X3 موجودی جدید من و X4 موجودی جدید شما» دارید. میخواهید گواهی ایجاد کنید که این تراکنش صحیح است (به طور مشخص به نحوی که ثابت کند موجودیهای جدید و قدیم همگی مثبت هستند و کاهش موجودی یک طرف برابر با افزایش موجودی طرف دیگر است). x در اینجا میتواند یک زوج کلید رمزنگاری و f تابعی باشد که مقادیر تراکنش را گرفته، تراکنش را رمزگشایی کرده، بررسی را انجام داده و در صورت صحت عدد ۱ و در صورت وجود مشکل عدد صفر را بازگرداند. y در اینجا قاعدتا باید ۱ باشد.
- بلاک چینی همچون شبکه اتریوم دارید و میخواهید واپسین بلوک را دانلود کنید. گواهی نیاز دارید که ثابت کند این بلوک معتبر و آخرین بلوک زنجیرهای است که تمام بلوکهای آن معتبر هستند. از یک فول نود درخواست چنین گواهی میکنید. x در اینجا تمامی بلاک چین و f تابعی است که آن را بلوک به بلوک پردازش کرده و اعتبار آن را میسنجد و خروجی آن هش آخرین بلوک است. بنابراین در اینجا y باید برابر با هش بلوکی باشد که دانلود کردهاید.

پس قسمت مشکل این ماجرا در کجاست؟ به نظر میرسد که اطمینان بخشی از طریق ارائه گواه اثبات بینیاز به دانش چندان مشکل نیست؛ راههای مختلفی برای تبدیل هر نوع محاسباتی به شکلی همچون مساله گراف سه رنگ وجود دارد، به نحوی که رنگآمیزی گراف با سه رنگ مترادف با جواب مساله اصلی باشد. سپس از پروتکل سنتی گواه بینیاز به دانش برای اثبات اینکه رنگآمیزی صحیحی داریم – بدون افشای آن – استفاده خواهیم کرد. این مطلب عالی از متیو گرین (Matthew Green) که در سال ۲۰۱۴ نوشته شده است، این مطلب را با جزییات تشریح میکند.
قسمت پیچیدهتر ماجرا، ارائه گواهی موجز و مختصر است. اگر بخواهیم شهودی بگوییم، اثبات چیزی در خصوص اختصار محاسبات مشکل است چرا که محاسبات مفهومی به شدت شکننده است. اگر محاسبه سخت و طلانی داشته باشید که تنها با تغییر یک بیت، نتیجه کلی عوض شود، ایجاد نمونه رد محاسباتی تصادفی که بتوان اعتبار آن را ثابت کرد، بسیار مشکل میشود. اما خوشبختانه به کمک ریاضیات پیشرفته، میتوان این کار را انجام داد.
تفسیر عمومی و سطح بالای این مساله این است که پروتکلها به کمک ریاضیاتی مشابه آن چه در کدگذاری پاک کردن (Erasure Coding – EC) استفاده میشود، این کار را انجام میدهند. EC برای تحملپذیری خطا در دادهها به کار میرود. اگر مقداری داده در اختیار داشته باشید و آن را به شکل یک خط کد کنید، آن گاه میتوانید چهار نقطه بر روی خط برگزینید. هر دو نقطه از آن چهار نقطه برای بازسازی مجدد خط کافی است (به کمک معادله خط) و در نتیجه میتواند به شما مختصات آن دو نقطه دیگر را بدهد. اگر کوچکترین تغییری در داده ایجاد نمایید، آن گاه حداقل سه نقطه از آن چهار نقطه تضمین شده است. همچنین میتوانید داده را به شکل یک چندجملهای درجه ۱۰۰۰۰۰۰ کدگذاری کنید و دو میلیون نقطه بر روی چندجملهای برگزینید؛ در این صورت هر ۱۰۰۰۰۰۱ نقاط از آن نقطهها میتواند دادههای اصلی (و در نتیجه دیگر نقاط) را بازسازی کند و هر تغییری در داده اصلی سبب تغییر حداقل ۱۰۰۰۰۰۰ نقطه میشود. الگوریتمهایی که در اینجا به نمایش درخواهند آمد، از چندجملهایها برای تقویت خطا (Error Amplification) استفاده گستردهای مینمایند.
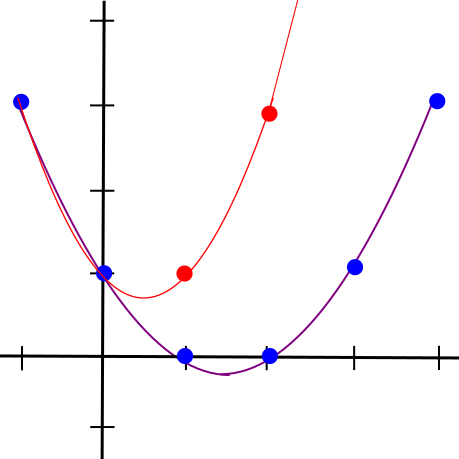
مثالی ساده از اثبات به کمک چندجملهایها
فرض کنید که میخواهید اثبات کنید که چندجملهای P را دارید به نحوی که P(x) دارای جوابی به فرم عدد صحیح بین ۰ تا ۹ برای xهای بین ۱ تا ۱ میلیون است. این نمونهای نسبتا ساده از فرایندی به نام بررسی برد (Range Checking) است؛ میتوانید یکی از کاربردهای چنین فرایندی را برای صحتسنجی و تایید مثبت بودن موجودی حسابها پس از انجام تراکنش در نظر بگیرید. اگر بررسی برای جوابهای ۱ تا ۹ باشد، میتوان آن را بررسی جوابهای صحیح یک جدول سودوکو در نظر گرفت.
راه سنتی این اثبات این است که تمامی یک میلیون نقطه را رسم کنیم و با بررسی مقادیر برد، ثابت کنیم که در محدوده قرار دارد. اما هدف ما ایجاد گواهی است که بتوانیم اعتبار آن را در کمتر از یک میلیون گام بررسی کنیم. بررسی تصادفی مقادیر P فایدهای نخواهد داشت: جرا که همواره احتمال این وجود دارد که یک اثباتکننده متخاصم یک جواب برای P ارائه کند که در ۹۹۹۹۹۹ حالت، شرط را به درستی ارضا کند اما در یک مورد نادرست باشد. نمونهبرداری تصادفی چند مقدار، تقریبا همیشه این یک مقدار نادرست را شناسایی نخواهد کرد. حال چه باید کنیم؟
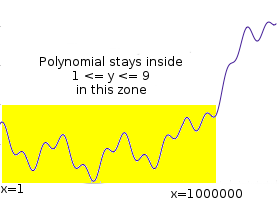
بیایید مساله را با تبدیل ریاضی تغییر دهیم. فرض کنید C(x) چندجملهای بررسی قیود باشد؛ این چندجملهای اگر x بین صفر تا ۹ باشد جواب صفر و در غیراین صورت غیرصفر خواهد بود. راه سادهای برای ساخت این چندجملهای وجود دارد. فرض میکنیم که تمامی چندجملهایهای ما و دیگر مقادیر، اعداد صحیح هستند و نیازی نیست که در خصوص اعداد مابین نگران باشیم. خواهیم داشت:
C(x):x.(x-1)(x-2)…(x-9)
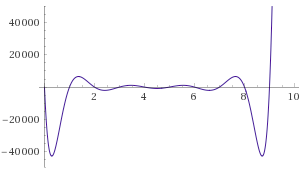
حال مساله بدل به این میشود: ثابت کنید که P را میدانید بدین ترتیب که برای همه xهای بین ۱ تا ۱۰۰۰۰۰۰، C(P(x)) = 0. حال Z(x) = (x-1)(x-2)…(x-1000000) تعریف میکنیم. اصل شناختهشده ریاضیای وجود دارد که هر چندجملهای که در تمامی xهای بین ۱ تا ۱۰۰۰۰۰۰ صفر باشد، باید مضربی از Z(x) باشد. بنابراین میتوانیم دوباره مساله را تبدیل کنیم: ثابت کنید که از مقدار P و D اطلاع دارید با این شرط که C(P(x)) = Z(x).D(x) باشد (برای تمامی مقادیر x). توجه داشته باشید که اگر شما C(P(x)) مناسبی بشناسید، تقسیم آن بر Z(x) برای محاسبه D(x) چندان مشکل نیست؛ برای این کار میتوانید از تقسیم چندجملهای بلند یا از الگوریتمی بهتر همچون تبدیل فوریه سریع استفاده کنید. این گونه ما ادعای اولیه خود را به چیزی که از لحاظ ریاضی مرتب و اثبات آن نسبتا آسان است تبدیل کردیم.
حال چگونه میتوان این ادعا را اثبات کرد؟ میتوانیم فرایند اثبات را یک پروسه ارتباط سه مرحلهای بین اثباتکننده (Prover) و اعتبارسنج (Verifier) ببینیم: اثباتکننده مقداری اطلاعات میفرستد، سپس اعتبارسنج چند درخواست بازمیگرداند، در نهایت اثباتکننده اطلاعات بیشتری میفرستد. ابتدا اثباتکننده یک درخت مرکل از ارزیابی مقادیر P(x) و D(x) برای xهای بین ۱ تا ۱ میلیارد (بله، میلیارد و نه میلیون) و هش ریشه آن میسازد و برای اعتبارسنج میفرستد. این جوابها شامل یک میلیون نقطهای که P(x) بین صفر تا ۹ است به علاوه ۹۹۹ میلیون نقطه دیگر که احتمالا در این شرط نمیگنجند است.
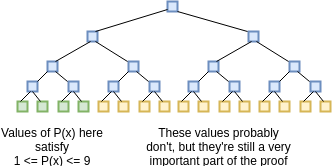
فرض میکنیم که اعتبارسنج جواب تمامی بررسی Z(x) در تمامی این نقاط را میداند؛ تابع Z(x) همانند کلید عمومی اعتبارسنجی برای این روش است که تمامی افراد باید از قبل بدانند (کلاینتهایی که توان ذخیرهئازی تمامی Z(x) را ندارند میتوانند ریشه مرکل Z(x) را ذخیره کنند و از اثباتکننده بخواهند تا شاخه Z(x) مدنظر اعتبارسنج را فراهم آورد؛ همچنین به روشی متفاوت، چندین میدان عددی بر Z(x) وجود دارد که xای مشخص را میتوان به راحتی محاسبه کرد). پس از دریافت تعهد (=ریشه مرکل)، اعتبارسنج سپس ۱۶ مقدار تصادفی x بین ۱ تا ۱ میلیارد را انتخاب میکند و از اثباتکننده میخواهد تا شاخه مرکل P(x) و D(x) را فراهم آورد. اثباتکننده این مقادیر را تهیه میکند. اعتبارسنج سپس بررسی میکند که الف) این شاخهها با هش ریشه که پیشتر ارائه شده بود مطابقت داشته باشد و ب) C(P(x)) برابر با Z(x).D(x) در تمامی ۱۶ نقطه باشد.
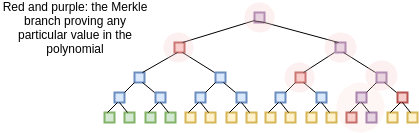
میدانیم که این گواه از نظر ریاضی کامل (Perfect Completeness) است – بدین معنی که اگر شما P(x) مناسبی سراغ داشته باشید،آن گاه میتوانید با محاسبه D(x) و ساخت گواه به شکل صحیح، از بررسی ۱۶ نقطه سربلند بیرون آیید. اما صحت یا استواری (Soundness) جواب چه؟ – بدین معنی که اگر یک اثباتکننده متخاصم تابع P(x) نادرستی ارائه کند، حداقل احتمالی که شناسایی خواهد شد چقدر است؟ میتوانیم این گونه بررسی کنیم. از آن جا که C(P(x)) یک چندجملهای درجه دهم است که با چندجملهای درجه ۱۰۰۰۰۰۰ ساخته شده است، حداقل درجه آن ده میلیون خواهد بود.به صورت کلی میدانیم که دو چندجملهای متفاوت با درجه N یکسان، حداکثر در N نقطه با یکدیگر یکسان هستند: بنابراین بنابراین یک چندجملهای درجه ده میلیون که با هیچ چندجملهای که برابر با Z(x).D(x) برای برخی از xها باشد، برابر نباشد در حداقل ۹۹۰ میلیون نقطه با آنها اختلاف خواهد داشت. بنابراین احتمال اینکه یک P(x) نادرست تنها در یک بار آزمون رد شود ۹۹٪ است؛ با ۱۶ آزمون، احتمال شناسایی یک پاسخ نادرست به «یک منهای ۱۰ به توان منفی ۳۲» افزایش پیدا میکند. بنابراین احتمال شکست چنین روشی به اندازه احتمال شکست تابع هش خواهد بود.
در عمل چه کردیم؟ از چندجملهایها برای افزایش خطا در هر راهحل نادرستی بهره جستیم تا هر پاسخ نادرست برای مساله اصلی به جای آن که به یک میلیون بار بررسی برای کشف احتیاج داشته باشد، در همان آزمون اول به احتمال ۹۹ درصد بتواند پاسخ نادرست را شناسایی کند.
میتوانیم سه گام شرح داده شده را به گواه غیرتعاملی (non-interactive proof) تبدیل کنیم؛ گواهی که میتواند توسط یک اثباتکننده تک ارسال شده و توسط همه صحتسنجی شود. برای این کار میتوان از میانبر فیات-شمیر استفاده کرد. اثباتکننده در ابتدا درخت مرکلی از مقادیر P(x) و D(x) میسازد و سپس هش ریشه آن را محاسبه میکند. از این ریشه سپس به عنوان عامل آنتروپی استفاده میشود تا شاخههایی از درخت که باید توسط اثباتکننده فراهم شود، تعیین شوند. اثباتکننده سپس ریشه مرکل و شاخهها را همراه با گواه ارائه میدهد. تمامی محاسبات در سمت اثبیاتکننده صورت میپذیرد: فرایند محاسبه ریشه مرکل از داده و سپس استفاده از آن برای انتخاب شاخههایی که قرار است مورد وارسی قرار گیرند. از این رو نیاز به تعامل بین اثباتکننده و اعتبارسنج از بین میرود.
تنها کاری که یک عامل متخاصم بدون در اختیار داشتن P(x) صحیح میتواند انجام دهد، ساخت گواه به شکل پشت سرهم است تا بالاخره شانس به او رو کند. اما با احتمال صحت گفته شده، میلیاردها سال طول خواهد کشید تا بتواند گواهی نامعتبر ارائه دهد و قسر در رود.
گسترش این روش
برای نمایش قدرت این تکنیک، بیایید از آن برای انجام کاری کمتر متداول استفاده کنیم: اثبات اینکه شما عدد یک میلیونیوم دنباله فیبوناچی را میدانید. برای نیل به این هدف، ثابت خواهیم کرد که از چندجملهای P(x) که دربرگیرنده عدد xام دنباله فیبوناچی است، اطلاع داریم. در این مثال، دنباله چککننده محدودیت ما در سه مختصات x در گذر خواهد بود:
C(x_1,x_2,x_3 )=x_3- x_2- x_1
توجه داشته باشید که اگر برای تمام xها، C(P(x), P(x+1), P(x+2)) = 0 باشد، آنگاه P(x) نماینده دنباله فیبوناچی است.
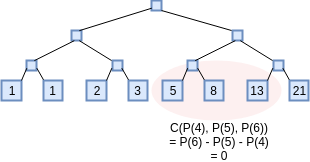
مساله را به شکل زیر میتوان ترجمه کرد: ثابت کنید که P و D را میدانید به نحوی که C(P(x), P(x+1), P(x+2)) = Z(x).D(x) باشد. برای تمامی ۱۶ اندیسی که اعتبارسنج خواهد سنجید، اثباتکننده باید شاخههای مرکل را برای P(x)، P(x+1)، P(x+2) و D(x) فراهم آورد.اثباتکننده همچنین باید به شکلی مجزا، شاخههای مرکلی که نشان میدهد P(0) = P(1) = 0 را ارائه کند. جز این، باقی فرایند مشابه قبل است.
برای اینکه در دنیای واقعی از این روش استفاده کنیم دو مشکل وجود دارد که باید حل شوند. مشکل اول این است که اگر بخواهیم از اعداد حقیقی برای راهحل استفاده کنیم، پاسخ چندان بهینه نخواهد شد چرا که اعداد به سرعت بسیار بزرگ خواهند شد. برای مثال، عدد یک میلیونیوم دنباله فیبوناچی، ۲۰۸۹۸۸ رقم دارد. اگر بخواهیم در عمل به موجز بودن برسیم، به جای استفاده از چندجملهایها با اعداد حقیقی، باید از میادین متناهی – سیستمی عددی که از قوانین حسابی یکسانی که میشناسیم و دوست داریم همچون a ⋅ ( b + c ) = ( a ⋅ b ) + ( a ⋅ c ) و ( a 2 − b 2 ) = ( a − b ) ⋅ ( a + b ) تبعیت میکند اما هر عدد میزان مشخصی از فضا را اشغال میکند – استفاده کنیم. بدین شکل، اثبات ادعاییی در خصوص عدد یک میلیونیوم دنبال فیبوناچی نیازمند طراحی پیچیدهتری است که از «حساب اعداد بزرگ» (Big Number Arithmetic) بر روی میادین متناهی سود میبرد.
سادهترین میدان متناهی ممکن، حساب پیمانهای است. در این روش، هر نمونهای از a + b را با مود (mod) a + b بر عدد اول N جایگزین میکنیم. همین کار را برای تفریق و ضرب نیز انجام میدهیم و برای تقسیم از وارون ضربی سود میجوییم. برای مثال اگر N هفت باشد، حاصل 3 + 4 برابر صفر، 2 + 6 = 1، 3 . 4 = 5، 4/2 = 2 و حاصل تقسیم ۵ بر ۲ برابر با ۶ خواهد شد.
ممکن است در اثبات «صحت» فوق، توجه کرده باشید که من یک از انواع حملات ممکن را پوشش ندادم: چه میشود اگر به جای P(x) درجه یک میلیون و D(x) درجه ۹ میلیون، عامل متخاصم مقادیری ارائه دهد که بر روی هیچ یک از این چندجملهایهای نسبتا درجه پایین نباشد؟ در این صورت، این استدلال که C(P(x)) نادرست باید متفاوت از هر C(P(x)) معتبر بر روی حداقل ۹۹۰ میلیون نقطه باشد، دیگر اعتباری نخواهد داشت. بنابراین حملات متفاوت و موثرتری قابل اجرا است. برای مثال، عامل متخاصم میتواند یک مقدار تصادفی p برای هر x تولید کند و سپس d = C(p)/Z(x) را محاسبه کند و این مقادیر را به جای P(x) و D(x) ارائه کند. این مقادیر بر روی هیچکدام از چندجملهایهای درجه پایین نیست، اما همچنان از آزمون موفق بیرون خواهند آمد.
از این احتمال میتوان به شکل موثر دفاع کرد، اما ابزار لازم برای چنین کاری پیچیده هستند و میتوان گفت اکثر نوآوری ریاضی STARKها مربوط به این حوزه است. افزون بر این، راهحل محدودیتی پیدا خواهد کرد: میتوانید پاسخهایی که بسیار از هر چندجملهای درجه یک میلیون، دور هستند را پاکسازی کنید (برای مثال، نیاز به تغییر ۲۰ درصد از کل مقادیر برای تبدیل آن به چندجملهای درجه یک میلیون دارید)، اما نمیتوانید پاسخهایی را که از یک چندجملهای تنها در یک یا دو مختصات متفاوت هستند، شناسایی کنید. بنابراین چیزی که این ابزارها مهیا میکنند گواه نزدیکی (Proof of Proximity) است – گواهی که اکثر نقاط P و D، متناظر با چندجملهای صحیحی هستند.
میتوان دزیافت که با وجود این مسائل، همچنان امنیتی کافی برای ارائه گواه وجود دارد، گرچه دو تغییر باید به وجود آید: ابتدا، در این حالت اعتبارسنج باید اندیسهای بیشتری را وارسی کند تا خطایی که این محدودیت ایجاب میکند، را خنثی سازد. مورد دوم این است که اگر مقدار مرزی در مساله داریم و آن را مورد بررسی قرار میدهیم (برای مثال، P(0) = P(1) = 1 در مساله بالا)، آن گاه نه تنها باید ثابت کنیم که اکثر نقاط بر روی یک چندجملهای هستند، بلکه باید مشخصا ثابت کنیم که آن دو نقطه خاص (یا به هر تعداد محدودیت مقدار مرزی که داشته باشیم) بر روی آن چندجملهای هستند.
جمعبندی
ویتالیک بوترین در این مطلب مبانی گواه اثبات بینیاز از دانش (ZK-STARK) را شرح میدهد و ما را با نحوه عمل این فناوری آشنا میکند. در این پروسه، به کمک چندجملهایها، میادین متناهی، مسائل بهینهسازی چندمتغیره و رمزنگاری، بی نیاز از افشای اطلاعات، میتوانیم وجود/دانایی خود نسبت به آن را ثابت کنیم. این مطلب شماره نخست، از مقالات سه بخشی ویتالیک بوترین در این خصوص است. در هفتههای آتی، با دو شماره دیگر با شما خواهیم بود.
آیا تاکنون از ZKها در زندگی عادی خود استفاده کردهاید؟ آیا با رواج این فناوری، صحته ارزهای دیجیتال و زندگی عادی دستخوش تغییر خواهد شد؟













