کریپتو با ویتالیک؛ همه‌چیز در مورد برنامه‌ حسابی درجه دوم (QAP)

ویتالیک بوترین یکی از بنیانگذاران اصلی شبکه اتریوم و از بزرگترین و تاثیرگذارترین متفکران حوزه بلاکچین است. به همین دلیل در میهن بلاکچین بر آن شدیم تا با ترجمه مقاله‌های بوترین به شکل دنباله‌دار، دیدگاه‌های او در خصوص موارد مختلف این حوزه را در اختیار علاقه‌مندان بگذاریم. پست‌های بلاگ شخصی او در طی سالیان، به نوعی نمایانگر سیر تکنولوژی بلاکچین نیز است و خواندن آن خالی از لطف نیست. مقاله پیش رو در خصوص نحوه کار یکی از فناوری‌های اثبات بی‌نیاز به دانش (اثبات با دانش صفر – Zero Knowldege Proof) با نام zk-SNARK است و در این مقاله ویتالیک بوترین، فرایند پیچیده این کار را به شکلی شیوا بیان می‌کند.

ویتالیک در این مقاله نحوه ساخت آزمونی که فناوری zk-SNARK از آن برای سنجش صحت اطلاعات استفاده می‌کند، شرح می‌دهد.

اخیرا علاقه زیادی در رابطه با فناوری پیرامون zk-SNARK در میان جامعه بلاکچین به وجود آمده است و افراد متعددی سعی در روشن‌سازی چیزی که اخیرا به پیچیدگی شهره شده است، داشته‌اند. فهم zk-SNARKها حقیقتا امری چالش‌برانگیز است، به خصوص آن که تعداد قطعات متحرکی که نیاز است همگی به کار افتند تا نتیجه نهایی به دست آید، بسیار زیاد است. اما اگر سعی کنیم تکنولوژی به کار رفته را به قطعات کوچک‌تر تقسیم کنیم، دریافت آن آسان‌تر می‌شود.

هدف از نوشتن این پست تشریح کامل zk-SNARKها نیست. در این مطلب فرض می‌شود که ۱) شما می‌دانید آن‌ها چیستند و چه می‌کنند و ۲) به اندازه کافی از علم ریاضی سر در می‌آورید تا بتوانید مفهوم چندجمله‌ای‌ها را به خوبی درک کنید (اگر عبارت P(x) + Q(x) = (P + Q)(x) که در آن P و Q چند جمله‌ای هستند برای شما واضح و آشکار است، در سطح مناسبی برای این مطلب قرار دارید). این مقاله سعی خواهد کرد تا به تشریح بخش اول نحوه کار اسنارک‌ها، آن طور که توسط اران ترومر (Eran Tromer) – محقق این حوزه – ترسیم شده است، بپردازد:

قدم‌های اشاره شده در تصویر بالا را می‌توان به دو بخش کلی تقسیم کرد: پیش از هر چیز باید توجه داشت که ZK-SNARKها را نمی توان به هر مساله محاسباتی به شکل مستقیم اعمال کرد بلکه در ابتدا باید مساله را به فرم مناسب درآورید تا بتوان عملیات خواسته شده را بر روی آن انجام داد. فرم اشاره شده «برنامه حسابی درجه دوم – Quadratic Arithmetic Program» نام دارد و تبدیل کد یک تابع به چنین فرمی خود پاسخی غیر بدیهی دارد. در کنار پروسه تبدیل کد تابع به فرم QAP، پروسه دیگری وجود دارد که می‌توان آن را موازی با آن اجرا کرد که در صورت پیدا کردن ورودی مناسب به کد، بتوانید پاسخی متناظر با آن (که برخی اوقات گواهی بر QAP نامیده می‌شود) ایجاد کنید. پس از این مراحل، پروسه نسبتا پیچیده دیگری برای ساخت اثبات دانش صفر (اثبات بی‌نیاز به دانش Zero Knowledge Proof) برای گواه ذکر شده در مرحله قبل وجود دارد و همچنین فرایند مجزای دیگری برای تایید اعتبار اثبات ارائه شده به شما از جانب فرد دیگر وجود دارد. اما موارد ذکر شده خارج از حوزه بحث این مطلب است.

مثالی که از آن برای نشان دادن این مراحل استفاده کنیم، مثالی ساده است. x^3 + x + 5 = 35 (راهنمایی: جواب این معادله ۳ است). این مساله به اندازه‌ای ساده است که QAP ایجاد شده آنقدر بزرگ نباشد که ترسناک به نظر آید اما به اندازه‌ای غیربدیهی است که بتوانید تمامی مراحل در کار را مشاهده کنید.

بیایید تابع‌مان را به شکل زیر تعریف کنیم:

def qeval(x):

    y = x**3

    return x + y + 5

زبان برنامه‌نویسی ساده و ویژه‌ای که بدین منظور این‌جا از آن استفاده می‌کنیم اعمال حسابی ساده (/، .، -، +)، به توان رساندن ثابت (x^7 پذیرفته است اما x^y نه) و تخصیص متغیر -که به اندازه کافی قدرتمند است که بتوانید به شکل نظری هر محاسبه‌ای را درون آن انجام دهید (به شرط آن که تعداد قدم‌های محاسباتی محدود باشد چرا که استفاده از حلقه مجاز نیست) – پشتیبانی می‌کند. توجه داشته باشید که از عملگر پیمانه‌ای (Modulo) و عملگرهای رابطه‌ای (بزرگتر، کوچکتر، بزرگتر مساوی، کوچکتر مساوی) پشتیبانی نمی‌شود چرا که راه بهینه‌ای برای انجام مقایسه یا پیمانه به شکل مستقیم با اعمال ریاضی محدود وجود ندارد. بدین خاطر شاکر باشید چرا که اگر چنین نبود قبل از اینکه بتوانید «ف» را در کلمه «فرحزاد» به زبان آورید، رمزنگاری مبتنی بر منحنی‌های بیضوی شکسته می‌شد.

می‌توان به کمک تشریح بیتی (bit decompositions) به عنوان ورودی کمکی – برای مثال  13 = 2^3 + 2^2 + 1– عملگر پیمانه‌ای و رابطه‌ای را به زبان مورد اشاره افزود و درستی تشریح را ثابت کرد و عملیات ریاضی را در مدارهای دودویی (باینری) انجام داد. همچنین در ریاضیات میدان متناهی (finite field arithmetic) چک کردن تساوی (==) ممکن است و در واقع کمی آسان‌تر است اما وارد جزییات این مسائل نخواهیم شد. می‌توانیم زبان مورد بحث را کمی گسترش دهیم تا از جملات شرطی (برای مثال اگر  x < 5: y = 7; در غیر این صورت y = 9 ) نیز پشتیبانی کند. این کار را با تبدیل شروط به فرم ریاضی می‌توان انجام داد: y = 7 ⋅ ( x < 5 ) + 9 ⋅ ( x ≥ 5 )

دقت کنید که هر دو مسیر این جملات شرطی اجرا خواهند شد بنابراین اگر تعداد زیادی شرط داشته باشید می‌تواند منجر به ایجاد سربار شود.

گام به گام این فرایند را طی خواهیم کرد. اگر می‌خواهید این کار را شخصا انجام دهید، کامپایلری برای این کار تهیه کرده‌ام که صرفا برای اهداف آموزشی تهیه شده است و هنوز آماده ساخت QAP برای zk-SNARKهای دنیای واقعی نیست!

تخت‌سازی

اولین گام در مسیر، طی نمودن فرایند تسطیح (Flattening) است که در آن کد اصلی را که ممکن است شامل عبارات پیچیده باشد به فرم مجموعه عباراتی که تنها به دو فرم زیر است، ‌تبدیل می‌کنیم:

x = y که در آن y می‌تواند متغیر یا عدد باشد.

x = y (op) z  که در آن op می‌تواند چهار عمل اصلی ریاضی (ضرب نقطه‌ای، جمع، تقسیم و تفاضل) و y و z می‌توانند متغیر، عدد و یا خود عبارات دیگر باشند.

می‌توانید هر یک از این عبارات به شکل یک گیت منطقی در مدار تجسم کنید. نتیجه عمل تسطیح برای کد بالا به شکل زیر است:

sym_1 = x * x

y = sym_1 * x

sym_2 = y + x

~out = sym_2 + 5

اگر کد اصلی و کد بالا را بخوانید متوجه می‌شوید که معادل یکدیگر هستند.

گیت‌هایی به سیستم‌های محدود مرتبه اول (R1CS)

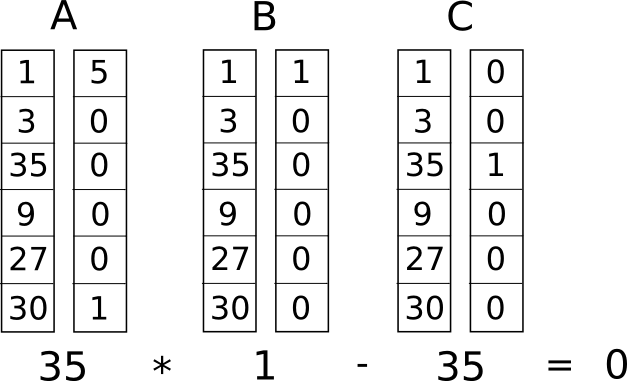
حال باید این عبارات را به چیزی که آن را سیستم محدود مرتبه اول (Rank-1 Constraint System) می‌نامیم تبدیل کنیم. یک R1CS عبارتی متشکل از سه بردار (a, b, c)  است و پاسخ آن بردار  

s است که s  باید شرط s . a ⋅ s . b − s . c = 0 برآورده سازد. ضرب داخلی (برداری) مجموع حاصل ضرب درایه‌های متناظر دو بردار در یکدیگر است. برای مثال، در تصویر زیر نمونه‌ای عددی از معادله بالا را مشاهده می‌کنید:

اما به جای داشتن تنها یک محدودیت،‌ با محدودیت‌های بسیاری مواجه خواهیم شد: به ازای هر گیت منطقی یکی. راه استانداردی برای تبدیل یک گیت منطقی به سه بردار (a, b, c) با توجه به نوع عملیات ریاضی و اینکه آرگومان‌ها متغیر یا عدد هستند وجود دارد. طول هر بردار برابر با تعداد کل متغیرهای سیستم با احتساب متغیر ساختگی – آن که در آرایه اول متناظر با عدد یک است – متغیرهای ورودی، یک متغیر ساختگی ~out که نماینده خروجی است و سپس تمام متغیرهای واسطه (sym1 و sym2 در مثال بالا) است. عموم بردارها بیشتر شامل درایه‌های صفر خواهند بود و تنها در جایگاه‌هایی متناظر با متغیرهایی که متاثر از گیت‌های منطقی می‌شوند، شامل عددی دیگر خواهند بود.

ابتدا نگاشت متغیرها را تهیه می‌کنیم:

‘~one’, ‘x’, ‘~out’, ‘sym_1’, ‘y’, ‘sym_2’

بردار پاسخ شامل این متغیرها به ترتیب ذکر شده خواهد بود.

حال ضرب سه‌گانه برداری را برای بردار (a, b, c) تشکیل می‌دهیم تا گیت اول را بسازیم:

a = [0, 1, 0, 0, 0, 0]

b = [0, 1, 0, 0, 0, 0]

c = [0, 0, 0, 1, 0, 0]

همان طور که می‌توانید مشاهده کنید اگر بردار پاسخ شامل عدد ۳ در جایگاه دوم و عدد ۹ در جایگاه چهارم باشد، فارغ از باقی محتویات بردار، حاصل ضرب نقطه‌ای همیشه 3 . 3 = 9 خواهد شد و از آزمون سربلند بیرون خواهد آمد. همچنین اگر بردار پاسخ شامل ۳- در جایگاه دوم و ۹ در جایگاه چهارم باشد، تساوی همچنان برقرار خواهد ماند. در واقع حتی اگر بردار جواب دارای عدد ۷ در جایگاه دوم و عدد ۴۹ در جایگاه چهارم باشد، همچنان همه‌چیز درست خواهد بود. هدف از این چک اولیه تنها تایید ورودی‌ها و خروجی‌های گیت اول است.

حال به سراغ گیت دوم می‌رویم:

a = [0, 0, 0, 1, 0, 0]

b = [0, 1, 0, 0, 0, 0]

c = [0, 0, 0, 0, 1, 0]

مشابه آزمونی که با ضرب نقطه‌ای برای گیت اول انجام دادیم، در اینجا حاصل sym1 . x = y را بررسی می‌کنیم.

اکنون به سراغ گیت سوم می‌رویم:

a = [0, 1, 0, 0, 1, 0]

b = [1, 0, 0, 0, 0, 0]

c = [0, 0, 0, 0, 0, 1]

در اینجا الگو کمی متفاوت است: در اینجا المان اول بردار پاسخ در المان دوم ضرب شده و سپس در المان پنجم ضرب می‌شود و جواب‌ها با یکدیگر جمع می‌شوند و بررسی می‌شود آیا پاسخ برابر با المان ششم هست یا نه. از آنجا که اولین المان در بردار پاسخ همواره یک است، این مرحله تنها یک آزمون جمع است که بررسی می‌کند آیا خروجی برابر با مجموع دو ورودی هست یا نه.

در نهایت گیت چهارم:

a = [5, 0, 0, 0, 0, 1]

b = [1, 0, 0, 0, 0, 0]

c = [0, 0, 1, 0, 0, 0]

در اینجا آخرین آزمون را ارزیابی می‌کنیم: ~out = sym2 + 5 . آزمون ضرب نقطه‌ای در این مورد بدین شکل کار می‌کند که المان ششم در بردار جواب را گرفته، پنج برابر المان اول (یادآوری: المان اول همیشه یک است بنابراین به معنی اضافه کردن عدد پنج است) را بدان اضافه می‌کند و آن را با المان سوم مقایسه می‌کند که جایی است که ما متغیر خروجی را در آن ذخیره می‌کنیم.

بدین ترتیب توانستیم چهار محدودیت R1CS خود را بسازیم. «گواه یا شاهد» متشکل از تناظر موارد بحث شده به تمامی متغیرها شامل ورودی، خروجی و متغیرهای واسطه است:

[1, 3, 35, 9, 27, 30]

می‌توانید کد تخت شده بالا را خودتان اجرا کنید؛ از جایگذاری x = 3 شروع کنید و سپس تمامی مقادیر متغیرهای واسطه و خروجی را مطابق محاسبه خودتان جایگذاری کنید.

R1CS تکمیل شده به شکل زیر است:

A

[0, 1, 0, 0, 0, 0] [0, 0, 0, 1, 0, 0] [0, 1, 0, 0, 1, 0] [5, 0, 0, 0, 0, 1]

B

[0, 1, 0, 0, 0, 0] [0, 1, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0]

C

[0, 0, 0, 1, 0, 0] [0, 0, 0, 0, 1, 0] [0, 0, 0, 0, 0, 1] [0, 0, 1, 0, 0, 0]

از R1CS به QAP

قدم بعدی تبدیل این سیستم محدود مرتبه اول به فرم QAP است که از منطق مشابهی پیروی می‌کند تنها تفاوت آن استفاده از چندجمله‌ای‌ها به جای ضرب نقطه‌ای است. چنین عمل می‌کنیم: چهار گروه سه برداری به طول شش را به شش گروه سه تایی از چند جمله‌ای درجه سه تیدل می‌نماییم که در آن ارزیابی چندجمله‌ای‌ها در هر مختصات ایکس، نماینده یکی از محدودیت‌هاست. برای نمونه اگر ما چندجمله‌ای‌ها را در مختصات x = 1 بررسی کنیم، مجموعه اول از بردارهایمان را خواهیم داشت. اگر آن‌ها را در x = 2 بررسی کنیم، گروه دوم و به همین ترتیب تا آخر.

می‌توانیم این تبدیل را به کمک درونیابی لاگرانژ انجام دهیم. مساله‌ای که به کمک درونیابی لاگرانژ حل می‌شود به شرح زیر است: اگر شما مجموع نقاطی به مختصات ایکس و ایگرگ داشته باشید و سپس درونیابی لاگرانژ را بر روی آن‌ها اعمال کنید، حاصل یک چندجمله‌ای خواهد بود که از تمامی این نقاط می‌گذرد. این امر را به کمک شکستن مساله انجام می‌دهیم: برای هر مقداری از x، ابتدا یک چندجمله‌ای ایجاد می‌کنیم که مقدار y مورد نظرمان را در آن x خاص برآورده می‌سازد و برای دیگر مقادیر x، مقدار y آن صفر است. سپس این کار را برای تمامی مقادیر دیگر ایکس به صورت مجزا انجام می‌دهیم و تمامی چندجمله‌ای‌های حاصل را با یکدیگر جمع می‌کنیم.

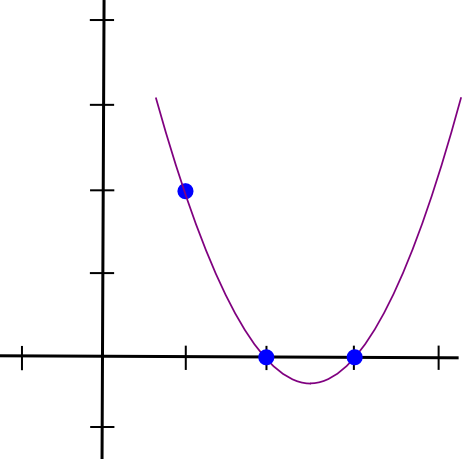
بیایید با یک مثال بررسی کنیم. فرض کنید که چندجمله‌ای می‌خواهیم که از نقاط (1, 3)، (2, 2) و (3, 4) بگذرد. با ساخت چندجمله‌ای که از نقاط (1, 3)، (2, 0) و (3, 0) بگذرد کار را آغاز می‌کنیم. ساخت چندجمله‌ای که تنها در x = 1 مقدار داشته باشد و در دیگر نقاط مدنظر ما صفر باشد آسان است. می‌توانیم به راحتی بنویسیم:

(x – 2) * (x – 3)

که شکل آن مطابق نمودار زیر است:

حال تنها باید کمی آن را فشرده کنیم تا ارتفاع آن در x = 1 صحیح باشد:

(x – 2) * (x – 3) * 3 / ((1 – 2) * (1 – 3))

این در نهایت منجر به ایجاد چند جمله‌ای زیر می‌شود:

1.5 * x**2 – 7.5 * x + 9

همین کار را برای دو نقطه دیگر انجام می‌دهیم و دو چندجمله‌ای نسبتا مشابه حاصل می‌شود. با جمع سه چندجمله‌ای با یکدیگر، تابع زیر حاصل می‌شود:

1.5 * x**2 – 5.5 * x + 7

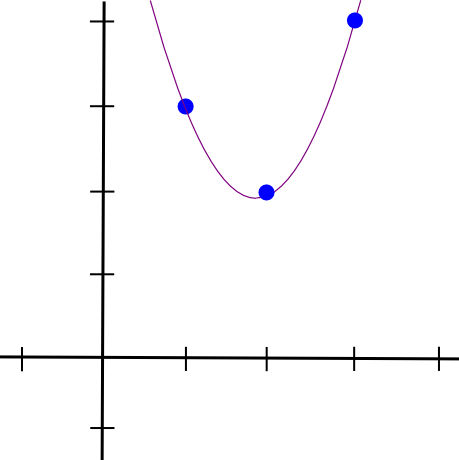
همان‌طور که از نمودار آن مشاهده می‌کنید، دقیقا مختصات دلخواه ما را برآورده می‌سازد. الگوریتمی که برای مثال فوق آن را شرح دادیم، O(n^3) بار گام برای تولید احتیاج دارد چرا که n نقطه وجود دارد و هر نقطه نیازمند O(n^2) بار ضرب چندجمله‌ای ها با یکدیگر است. با کمی تفکر می‌توان این مقدار را به O(n^2) بار کاهش داد و با فکر بیشتر و سود جستن از الگوریتم‌های تبدیل فوریه سریع و امثالهم این زمان و گام‌ها را حتی می‌توان بیشتر کاهش داد. این بهینه‌سازی در توابع دنیای واقعی بسیار مهم است چرا که در عمل zk-SNARKها با هزاران گیت منطقی سر و کار دارند.

حال بیایید از درونیابی لاگرانژ برای تبدیل R1CS خود استفاده نماییم. کاری که خواهیم کرد این است که اولین مقدار هر بردار a را گرفته و با استفاده از درونیابی لاگرانژ یک چندجمله‌ای از آن می‌سازیم (که در این روند، ارزیابی هر چندجمله‌ای در i به شما اولین مقدار بردار _ia ام را می‌دهد)، سپس این پروسه را برای اولین مقدار هر بردار b و c تکرار می‌کنیم و بعد این کار را برای دومین و سومین و…مقادیر هر بردار تکرار می‌نماییم. برای راحتی، مقادیر نهایی را برای شما مهیا کردم:

A polynomials

[-5.0, 9.166, -5.0, 0.833] [8.0, -11.333, 5.0, -0.666] [0.0, 0.0, 0.0, 0.0] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5] [-1.0, 1.833, -1.0, 0.166]

B polynomials

[3.0, -5.166, 2.5, -0.333] [-2.0, 5.166, -2.5, 0.333] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0]

C polynomials

[0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [-1.0, 1.833, -1.0, 0.166] [4.0, -4.333, 1.5, -0.166] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5]

ضرایب به شکل صعودی هستند بنابراین اولین چندجمله‌ای بالا در واقع 0.833 ⋅ x 3 — 5 ⋅ x 2 + 9.166 ⋅ x − 5 است. این مجموعه از چندجمله‌ای‌ها (به همراه چند جمله‌ای Z که بعدا در مورد آن توضیح خواهم داد) پارامترهای QAP ما را در این مثال تشکیل می‌دهند. توجه کنید که تمامی اعمالی که تا این لحظه انجام دادیم تنها کافی است برای هر تابع در زمان استفاده از zk-SNARKها یک بار انجام شود تا بتوان اعتبارسنجی کرد: پس از آن که پارامترهای QAP تولید شد، می‌توان از آن‌ها دوباره استفاده کرد.

بیایید این چندجمله‌ای را در x = 1 ارزیابی کنیم. ارزیابی چندجمله‌ای در x = 1 به معنی جمع‌ کردن تمامی ضرایب است و کار دشواری نیست. خواهیم داشت:

A results at x=1

0

1

0

0

0

0

B results at x=1

0

1

0

0

0

0

C results at x=1

0

0

0

1

0

0

همانطور که از مقایسه با سه بردار بالا می توانید مشاهده کنید، جواب ما کاملا مشابه گیت‌های منطقی است که در بالا داشتیم.

چک کردن برنامه حسابی درجه دوم

فایده این تبدیل پیچیده چیست؟ پاسخ این است که حالا می‌توانیم به جای چک کردن تمام محدودیت‌ها به شکل تک به تک در R1CS، تمامی آن‌ها را همزمان با انجام ضرب نقطه‌ای بر روی چندجمله‌ای‌ها ارزیابی کنیم.

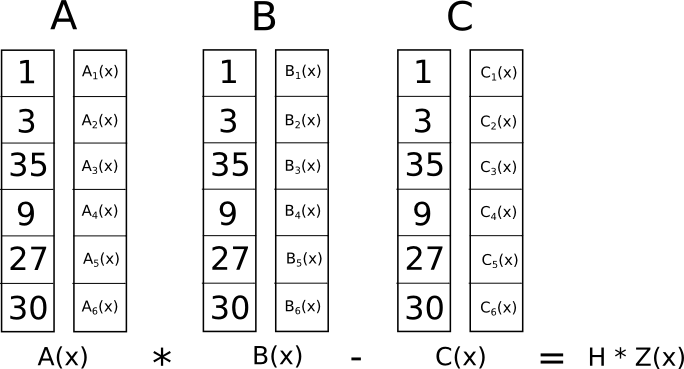
چون در اینجا حاصل آزمون ضرب نقطه‌ای ما مجموعه‌ای از جمع‌ها و ضرب‌های چندجمله‌ای‌هاست، جواب نیز یک چند جمله‌ای خواهد بود. اگر چندجمله‌ای حاصل به ازای هر مختصات ایکسی که می‌خواهیم نشانگر یک گیت منطقی باشد، مساوی صفر باشد، آن گاه بدین معنی است که از آزمون سربلند بیرون آمده است. اما اگر تنها در یکی از مقادیر ایکس که نماینده یک گیت منطقی است، جواب چندجمله‌ای برابر با صفر نشود، بدین معنی است که مقادیری که به این گیت وارد و خارج می‌شوند ثبات ندارند و درست نیستند.

دقت کنید که لازم نیست چندجمله‌ای حاصل خود صفر باشد و در واقع در اکثر اوقات چنین نخواهد بود. ممکن است در نقاطی که متناظر با گیت‌های منطقی نیستند هر رفتاری از خود نشان دهد اما مادامی که در نقاط مشخص شده جواب صفر حاصل شود، پاسخ ثبات دارد. برای تشخیص درستی، چندجمله‌ای را واقعا در تمامی نقاط متناظر با گیت‌های منطقی مشابه این فرمول (t = A . s ⋅ B . s − C . s) محاسبه نمی‌کنیم بلکه به جای آن t را تقسیم بر چندجمله‌ای دیگری به نام Z می‌کنیم و سپس چک می‌نماییم که آیا حاصل تقسیم باقی‌مانده‌ای از خود به جا می‌گذارد یا نه.

چندجمله‌ای Z به شکل چندجمله‌ای ساده‌ای تعریف می‌شود (( x − 1 ) ⋅ ( x − 2 ) ⋅ ( x − 3 ) . . .) که در تمامی نقاط متناظر با گیت‌های منطقی حاصل آن صفر است. اصل ساده‌ای در جبر وجود دارد که هر چندجمله‌ای که در تمامی نقاط مشابه حاصل صفر دارد، باید مضربی از این چند جمله‌ای مینیمال ساخته ما باشد و اگر چند جمله‌ای مضربی از Z باشد، آن گاه حاصل آن در تمامی نقاط مشابه صفر خواهد بود. این اصل، کار ما را بسیار ساده‌تر می‌سازد.

حال بیایید آزمون ضرب نقطه‌ای را برای چندجمله‌ای اشاره شده انجام دهیم. ابتدا چندجمله‌ای‌های واسطه:

A . s = [43.0, -73.333, 38.5, -5.166]

B . s = [-3.0, 10.333, -5.0, 0.666]

C . s = [-41.0, 71.666, -24.5, 2.833]

حال نوبت A . s ⋅ B . s — C . s است:

t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]

اکنون به سراغ چند جمله‌ای مینیمال Z می‌رویم. Z = ( x − 1 ) ⋅ ( x − 2 ) ⋅ ( x − 3 ) ⋅ ( x − 4 ):

Z = [24, -50, 35, -10, 1]

و اگر حاصل را بر Z تقسیم کنیم، خواهیم داشت:

h = t / Z = [-3.666, 17.055, -3.444]

که باقی‌مانده‌ای ندارد.

و این چنین پاسخ صحیح برای QAP را داریم. اگر تلاش کنیم که پاسخ به دست آمده از متغیرهای R1CS را خراب کنیم – برای مثال به جای ۳۰ عدد ۳۱ را در مقدار آخر قرار دهیم، آن گاه چندجمله‌ای حاصل در یکی از آزمون‌ها مردود می‌شود (به شکل دقیق‌تر در x = 3 به جای صفر، حاصل ۱- خواهد شد). همچنین دیگر چندجمله‌ای نهایی مضربی از Z نخواهد بود و حاصل تقسیم دارای باقی‌مانده‌ای به مقدار [ − 5.0 , 8.833 , − 4.5 , 0.666 ] خواهد بود.

توجه به این امر ضروری است که مثال بالا، نسخه ساده شده چیزی است که در عمل رخ می‌دهد. در دنیای واقعی جمع‌ها، ضرب‌ها و تفاضل‌ها با استفاده از اعداد طبیعی انجام نمی شود بلکه از المان‌های میدان محدود – بخشی از ریاضیات که تمام قوانین جبری که از آن استفاده می‌کنیم برقرار است اما تمامی پاسخ‌ها المان‌هایی از مجموعه‌ای متناهی هستند که معمولا اعدادی صحیح بین بازه صفر تا n-1 برای یک n مشخص هستند – استفاده می‌شود. برای مثال اگر n = 13 باشد، آنگاه 1 / 2 = 7، 7 ⋅ 2 = 1 ، 3 ⋅ 5 = 2 و به همین ترتیب. استفاده از ریاضیات المان‌های میدان محدود نیاز به نگرانی در خصوص خطاهای گرد شدن در محاسبات را از میان می‌برد و این اجازه را به سیستم می‌دهد تا به درستی با منحنی‌های بیضوی هماهنگ باشد که برای ادامه اعمالی که در zk-SNARKها صورت می‌پذیرد لازم و حیاتی است.