انفجار کامبری اثبات‌های کریپتو و سیستم‌های رمزنگاری پیشرفته و نوین!

مقاله زیر توسط الی بن‌ساسون (Eli Ben-Sasson) نوشته شده است. او رئیس هیئت مدیره پلتفرم استارک‌ور (StarkWare) و از بنیان‌گذاران زی‌کش است. این مقاله در وبسایت ناکاموتو منتشر شده است. 

این پست در مورد سیستم های اثبات کریپتو است و برای افرادی مناسب است که دارای پیشینه ای در رمزنگاری (cryptography) باشند. در اینجا به بررسی رمزنگاری در حال گسترش سیستم های اثبات و نقش STARKs متقارن در آنها پرداخته می شود. این نوشتار بر اساس یک سخنرانی است که در نوامبر ۲۰۱۹ و در سانفرانسیسکو (San Francisco) ارائه شده است. رمزنگاری مقوله ای بسیار مهم در جهان بلاک چین و ارز دیجیتال است.

مقدمه ای بر وضعیت کنونی جهان رمزنگاری

زمین ما برای حدودا ۳.۵ میلیارد سال مملو از جانداران تک سلولی بوده است و سپس در نتیجه یک تغییر زمین شناختی که به انفجار کامبری (Cambrian Explosion) معروف است، تقریبا همه نژاد حیواناتی که امروزه می شناسیم، ایجاد شده اند.

در زمینه اثبات های رمزنگاری صحت محاسباتی نیز ما در دوران انفجار کامبری به سر می بریم. در حالی که تا چند سال قبل، سالانه تنها شاهد ظهور ۱ تا ۳ سیستم بودیم، امروزه ماهانه و یا حتی هفتگی با این تعداد سیستم روبرو می شویم. هدف از این پست، شناسایی پایه های رایج همه این سیستم هاست که به سیستم های CI معروفند و به صورت کد پیاده سازی شده اند. در اینجا تعدادی از عوامل ایجاد کننده تمایز نیز مورد بحث قرار می گیرد.

توجه داشته باشید که این مقاله مقداری فنی است و مناسب افرادی است که دارای پیش زمینه ای در رمزنگاری هستند. البته خواندن آن برای افراد غیر فنی علاقه مند به زبان و اصطلاحات مورد استفاده در این حیطه نیز خالی از لطف نیست و سعی شده که مطالب به صورت خلاصه و ساده توضیح داده شود. هدف دیگر ما از نوشتن این مقاله، توضیح این است که چرا شرکت ما StarkWare، اهتمام خاصی به استفاده از منابع خود در شاخه ای از سیستم های CI با نام  STARKs متقارن دارد.

اجداد مشترک

سیستم های اثبات صحت محاسباتی می توانند به حل دو مشکل اساسی بلاک چین های غیر متمرکز کمک کنند که این دو مشکل، حریم خصوصی و مقیاس پذیری هستند. اثبات های دانش صفر (ZKPs)، حریم خصوصی را با محافظت از تعدادی از ورودی های یک محاسبه فراهم می کنند و در این میان، صحت را نیز به مخاطره نمی اندازند. سیستم های دقیق CI، مقیاس پذیری را نیز با فشرده سازی نمایی مقدار محاسبات مورد نیاز برای تایید صحت گروه بزرگی از تراکنش ها، فراهم می کنند.

همه این سیستم های CI که به صورت کد پیاده سازی شده اند، دارای دو ویژگی مشترک هستند. این دو ویژگی مشترک Arithmetization و مفهوم LDC هستند. Arithmetization به تقلیل اظهارات محاسباتی ایجاد شده توسط یک الگوریتم در حال اثبات گفته می شود.

مفهوم LDC نیز بدین معنی است که از رمزنگاری استفاده می شود تا مطمئن شوند که اثبات کننده چند جمله ای های درجه پایین را انتخاب می کند و آنها را در نقاط انتخاب شده تصادفی مورد ارزیابی قرار می دهد. البته این نقاط را تایید کننده درخواست کرده است.

با توجه به این موارد، CI را می توان بر طبق مبادی اولیه رمزنگاری مورد استفاده برای اجرای LDC، راه حل های LDC خاص که با آن مبادی اولیه ساخته شده است و نوع Arithmetization اجازه داده شده توسط این انتخاب ها، طراحی کرد. حال به شرح ابعاد مقایسه در این زمینه می پردازیم.

مفروضات رمزنگاری

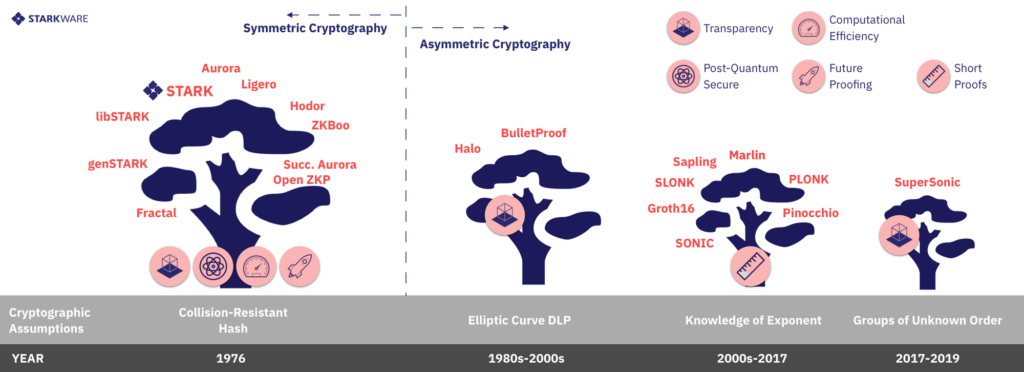
بزرگترین عامل متمایز تئوری در میان سیستم های CI مختلف این است که آیا امنیت آنها نیازمند مبادی اولیه متقارن و یا نامتقارن است؟ مبادی اولیه متقارن معمولی SHA2، SHA3 یا Blake می باشند. مفروضات نامتقارن نیز شامل چیز هایی مانند سختی حل مدول مشکل لگاریتمی مجزا، یک ضریب RSA و غیره است.

تقسیم متقارن و غیر متقارن بین سیستم های CI دارای پیامد های زیادی است که از جمله آنها می توان به موارد زیر اشاره کرد:

کارایی محاسباتی

امنیت مبادی اولیه نامتقارن که امروزه یه صورت کد پیاده سازی شده اند، نیازمند حل مشکلات LDC در حوزه های جبری عظیم است. از طرف دیگر، ساختار های متکی بر مفروضات متقارن به اجرای LDC در هر حوزه جبری می پردازند که شامل زیرمجموعه های همواری باشد. در نتیجه، سیستم های CI متقارن را می توان در هر زمینه ای محاسبه کرد و این منجر به کارایی عالی تری می شود.

امنیت پس کوانتومی (post-quantum)

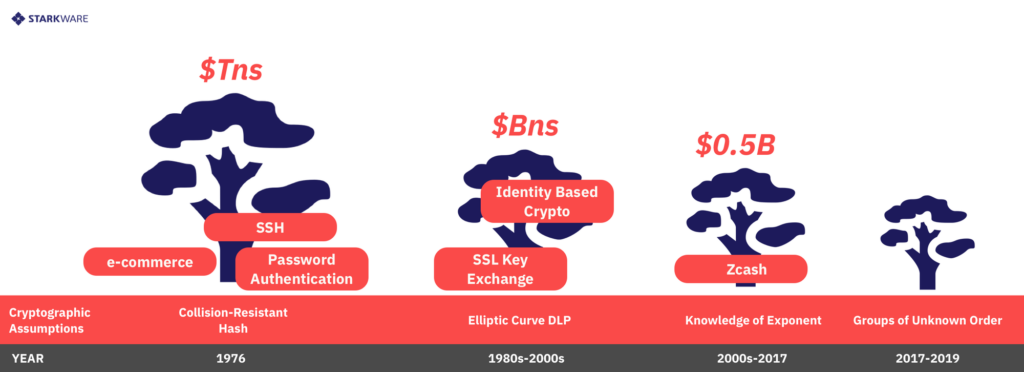
همه مبادی اولیه نامتقارن حال حاضر که در CI مورد استفاده قرار گرفته است را می توان توسط یک کامپیوتر کوانتومی شکست، که البته این کامپیوتر باید در حالتی باشد که به اندازه کافی بزرگ باشد. از طرف دیگر، مبادی اولیه متقارن احتمالا به صورت پس کوانتومی ایمن هستند. در نتیجه، تنها این سیستم های متقارن هستند که احتمالا به صورت پس کوانتومی ایمن هستند.

مقاومت در برابر گذشت زمان

همواره سیستم هایی که مبتنی بر چیز های قدیمی و اثبات شده هستند، در آینده بیشتر از سیستم های جدید باقی می مانند زیرا این سیستم های قدیمی امتحان خود را پس داده اند. سیستم های متقارن نیز در این میان قدیمی تر هستند و بیشتر مورد بررسی و آزمایش قرار گرفته اند و بنابراین پایداری بیشتری در آینده به نسبت سیستم های نامتقارن که جوان تر هستند، خواهند داشت.

همچنین سلسله مراتب ریاضیاتی سختی در میان این مفروضات موجود است. فرض CRH در این سلسله مراتب حکمرانی می کند زیرا اگر این فرض شکسته شود، مفروضات RSA و DLP هم شکسته خواهند شد و به این ترتیب می توان مثال های بیشتری زد. در نتیجه باید گفت که مفروضات نامتقارن جدید مبنای پر ریسک تری برای یک زیرساخت مالی هستند.

طول آرگومان (Argument Length)

همه نکاتی که تا به حال مطرح شده اند، به نفع ساختار های CI متقارن بوده اند. اما ساختار های نامتقارن در یک زمینه عملکرد بهتری دارند و آن پیچیدگی ارتباط یا همان طول آرگومان می باشد که به میزان یک تا سه واحد کوچکتر از ساختار های متقارن است. سیستم های نامتقارن دارای مدار خاص کوتاه تر از دیگر سیستم های نامتقارن و کوتاه تر از همه سیستم های متقارن هستند.

طرح های LDC

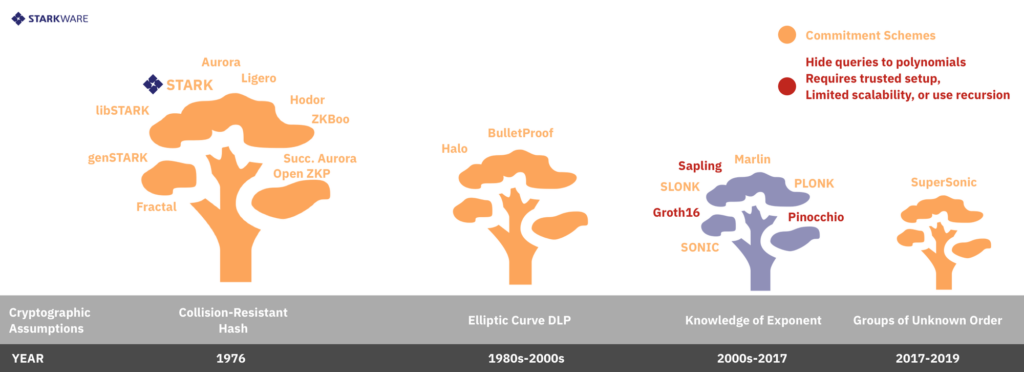
دو روش اصلی برای دستیابی به LDC وجود دارد که یکی از آنها مخفی کردن پرسش ها و دیگری طرح های تعهد می باشد که در ادامه به بررسی تفاوت های آنها می پردازیم.

روش اول مکانیسمی است که در زی کش (Zcash) مورد استفاده قرار می گیرد و بسیار ایمن است. در اینجا، آنچه که به اثبات کننده داده می شود، یک توالی از کدگذاری های توان است و اگر اثبات کننده مایل به تقلب باشد، به احتمال زیاد آشکار می شود. توجه داشته باشید که این سیستم به نوعی تعامل نیاز دارد و این تعامل به دلایل تئوری اجتناب ناپذیر است. این سیستم شفاف نیست و آنتروپی (entropy) مورد استفاده برای کدگذاری هویدا نیست.

در روش دوم لازم است که اثبات کننده مجموعه ای از چند فورمولی ها را اجرا کند که این کار با ارسال تعدادی پیام رمزنگاری شده برای تایید کننده انجام می گیرد. طبیعتا چنین طرح هایی متعامل و شفاف هستند. این شفافیت اجازه می دهد که پروتکل را به صورت غیر متعامل فشرده کرد و یا از منابع عمومی دیگر استفاده کرد. رایج ترین طرح در این روش، درختان مرکل (Merkle Trees) است و این روش احتمالا به صورت پس کوانتومی ایمن است. اما این روش منجر به طول آرگومان زیاد می شود. استفاده از طرح های تعهد نامتقارن دارای نقاط قوت و نقاط ضعف مخصوص به خود است.

Arithmetization

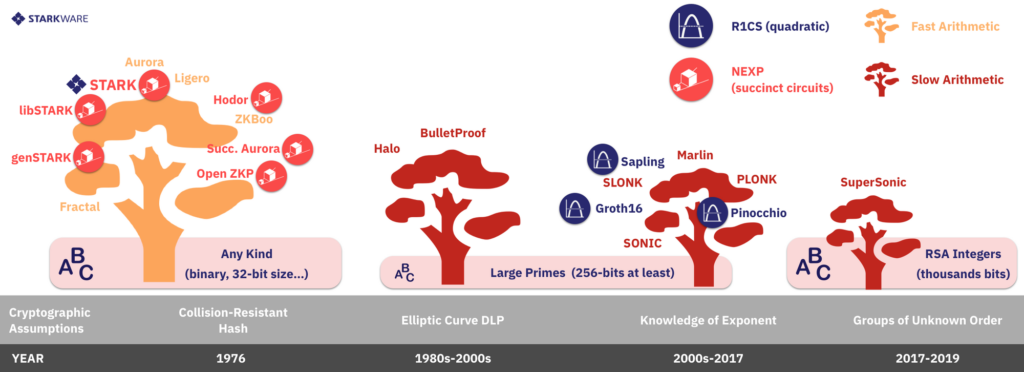
انتخاب فرض رمزنگاری و روش های LDC همچنین دامنه احتمالات arithmetization را به سه شیوه برجسته تحت تاثیر قرار می دهد که در شکل بالا نیز قابل مشاهده است.

۱-مدار های NP در برابر برنامه های NEXP

اکثر سیستم های CI پیاده شده، مشکلات محاسباتی را به مدار هایی حسابی تقلیل می دهند که سپس به یک مجموعه مانع تغییر می یابند. این رویکرد باعث بهینه سازی مدار های خاص می شود اما نیازمند یک فرد تایید کننده یا یک فرد معتمد است تا محاسبه انجام شود. این روش در مورد سیستم زی کش جواب می دهد. اما سیستم های مقیاس پذیر و شفاف مانند libSTARK، باید از یک ارائه فشرده محاسباتی استفاده کنند. اصطلاحات NP و NEXP نیز به ترتیب اشاره به این دو سیستم دارند.

۲-اندازه الفبا و نوع

می توان از مفروضات رمزنگاری برای تعیین این استفاده کرد که کدام حوزه های جبری می توانند به عنوان الفبایی که محاسبه می کنیم، عملکرد داشته باشند. به عنوان مثال، اگر از جفت سازی دو سویه استفاده کنیم، پس الفبایی که برای محاسبه به کار می بریم، یک گروه چرخه ای از نقاط منحنی بیضوی است و این گروه باید اندازه اولیه بزرگی داشته باشد و این یعنی که ما نیازمند محاسبه در این زمینه می باشیم. نوع فیلد (field) هم در اینجا اهمیت دارد زیرا فیلد های کوچکتر منجر به اثبات سریعتر و همچنین زمان تایید سریعتر می شوند.

۳-مانع های چند فورمولی عمومی در برابر R1CS

SNARK هایی که به سبک زی کش عمل می کنند، از جفت سازی های دوسویه بر روی منحنی های بیضوی استفاده می کنند تا به حساب کردن موانع محاسبه بپردازند. این استفاده خاص، محاسبه را به دریچه هایی محدود می کند که R1CS نام دارند. سادگی و فراگیری R1CS باعث شده که سیستم های دیگر نیز از آن استفاده کنند، اگرچه شکل های عمومی تری از موانع را می توان مورد استفاده قرار داد.

STARK در برابر SNARK

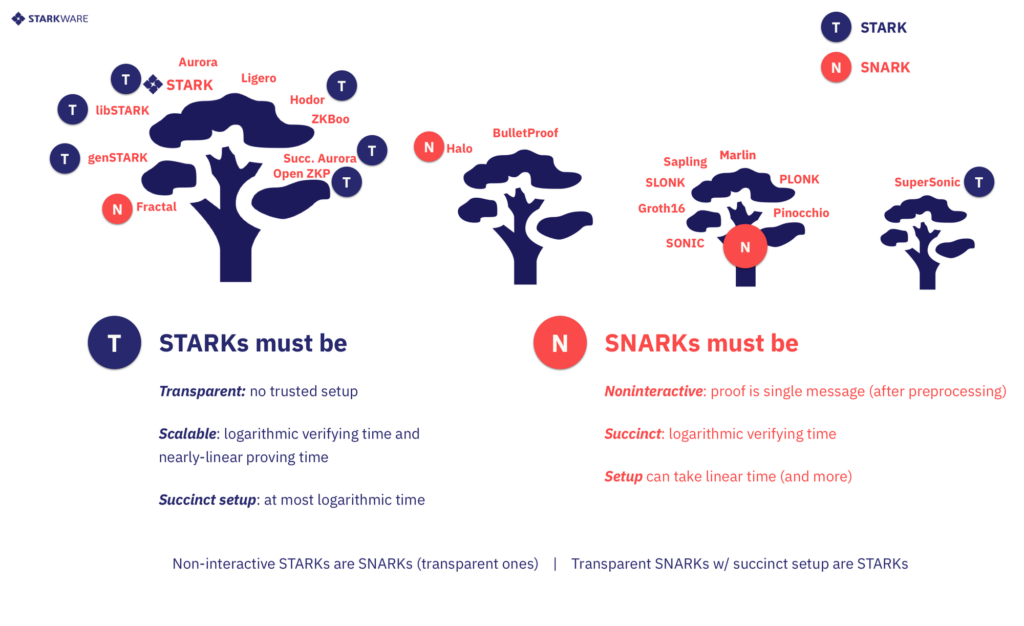
در اینجا موقعیت خوبی برای مشخص کردن تفاوت بین STARK و SNARK پیش آمده است. هر دوی این مفاهیم دارای تعاریف ریاضیاتی عینی هستند و ساختار های معینی را می توان به عنوان STARK یا SNARK و یا هر دو ارائه داد. این اصطلاحات بر ویژگی های مختلفی از سیستم های اثبات تاکید دارند. برای روشن تر شدن بحث به شکل بالا دقت کنید.

STARK

حرف S در اینجا برای کلمه scalability (مقیاس پذیری) آمده است که به این معنی است که با افزایش اندازه گروه، مقیاس های زمان نیز همزمان به صورت چند لگاریتمی تایید می شوند. T نیز حرف اول کلمه Transparency به معنی شفافیت می باشد و این یعنی که همه پیام های تایید کننده، کوین های تصادفی عمومی هستند. بر طبق این تعریف، اگر چیدمان قبل از پردازش موجود باشد، باید خلاصه باشد و تنها متشکل از کوین های تصادفی نمونه باشد.

SNARK

S در اینجا حرف اول کلمه succinctness به معنی خلاصه بودن است و این به معنی مقیاس های زمانی تایید کننده چند لگاریتمی است و N نیز حرف اول non-interactive به معنی غیر تعاملی است که این یعنی بعد از مرحله ماقبل پردازش، سیستم اثبات نمی تواند اجازه تعامل بیشتر را بدهد. توجه داشته باشید که بر طبق این تعریف، مرحله چیدمان امین خلاصه نشده مجاز است و در کل می توان گفت که لازم نیست که سیستم شفاف باشد.

SNARK از لحاظ تکامل کد بهتر از STARK است اما اگر به کاربرد های مقیاس پذیری علاقه مند هستید، STARK توصیه می شود و در حال حاضر STARK های متقارن بهترین هستند. و اگر شما می خواهید سیستمی بسازید که دارای کمترین مفروضات اعتماد باشد، از STARK متقارن استفاده کنید زیرا تنها اجزای مورد نیاز برای آن، CRH و یک منبع تصادفی عمومی است.

خلاصه

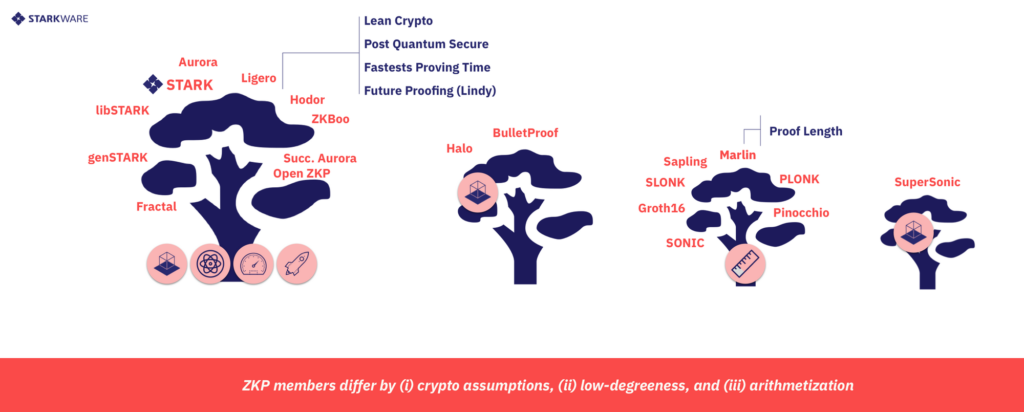
ما مفتخریم که در حال تجربه انفجار کامبری شگفت انگیز جهان سیستم های اثبات هستیم. قطعا ازدیاد این سیستم ها و نوآوری ها ادامه می یابد و ساختار ها و بینش های جدیدی ایجاد می شوند. بزرگترین خط تمایز در فضای سیستم های CI امروز، سیستم های نیازمند مفروضات رمزنگاری نامتقارن و سیستم های متکی بر مفروضات متقارن است که هر دوی این سیستم ها دارای مزیت ها و معایب خود هستند. بحث در مورد سیستم های آرگومان همچنان ادامه دارد. ما در شرکت StarkWare، برای آرگومان های کوتاه Groth 16 را توصیه می کنیم و برای بقیه چیز های دیگر، STARK های متقارن را توصیه می کنیم. نظر شما چیست؟ شما کدام سیستم رمزنگاری را می پسندید؟ نظرات خود را با ما در میان بگذارید.