کریپتو با ویتالیک؛ ساخت گواه بی نیاز به دانش به کمک حساب هم‌نهشتی

با شماره دیگری از «کریپتو با ویتالیک» با شما هستیم؛ در این مطلب که در اواخر سال ۲۰۱۷ نوشته شده است، بوترین شیوه ساخت گواه بی‌نیاز به دانش STARK را شرح می‌دهد. در صورتی که شماره قبلی را مطالعه نکردید، می‌توانید از باکس زیر به آن دسترسی داشته باشید:

همچنین اگر به دنبال توضیحی مقدماتی در خصوص گواه‌های اثبات بی‌نیاز به دانش (ZKP) و انواع مختلف آن هستید، این مقاله از میهن بلاکچین را مطالعه بفرمایید:

ساخت گواه بی‌نیاز به دانش STARK به شکلی بهینه

در قسمت نخست از سری بررسی ZK-STARK،‌ در خصوص چگونگی ساخت گواه اثبات محاسبات موجز صحبت کردیم؛ اثبات اینکه برای مثال عدد یک میلیونیوم از دنباله فیبوناچی را محاسبه کرده‌اید. این کار به کمک تکنیکی متشکل از ترکیب و تقسیم چندجمله‌ای‌ها صورت پذیرفت. با این وجود، این اثبات بر مرحله‌ای کلیدی استوار بود: توانایی اثبات اینکه حداقل، اکثریت مطلق مجموعه‌ای بزرگ از نقاط داده شده بر روی چندجمله‌ای درجه پایین یکسانی هستند. این مساله که «آزمون درجه پایین» (low-degree testing) نامیده می‌شود، احتمالا پیچیده‌ترین بخش پروتکل است.

بار دیگر کار را با شرح مجدد مساله آغاز می‌کنیم. فرض کنید که مجموعه‌ای از نقاط دارید و ادعا می‌کنید که تمامی آن‌ها بر روی چندجمله‌ای یکسانی قرار دارند که درجه‌ای کمتر از D دارند (برای مثال اگر درجه کوچک‌تر از ۲ باشد، بدین معنی است که بر روی یک خط قرار دارند و اگر کوچک‌تر از ۳ باشد بدین معنی است که بر روی یک خط یا منحنی قرار دارند). حال می‌خواهید گواهی احتمالی و موجز ارائه دهید که ثابت کند این مساله حقیقت دارد.

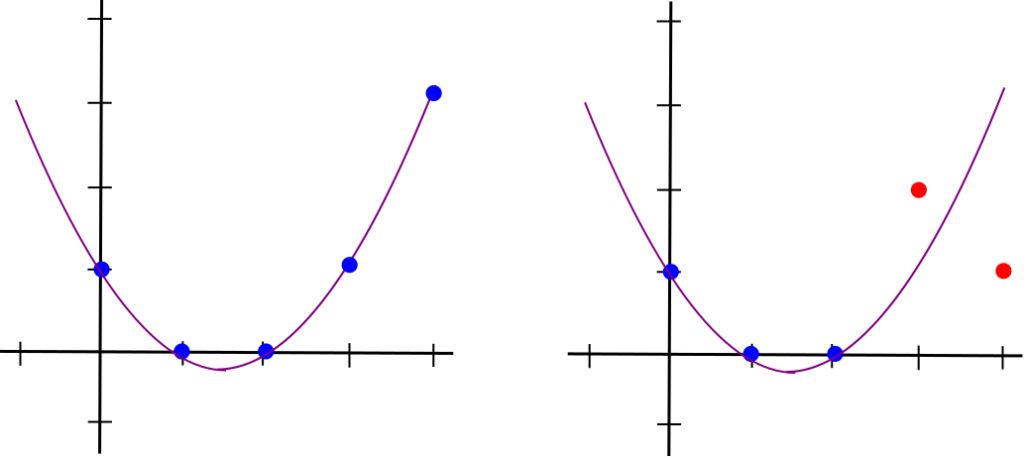
اگر بخواهید وجود تمام نقاط بر روی چندجمله‌ای با درجه کوچک‌تر از D را بررسی کنید، چاره‌ای جز بررسی تک‌تک نقاط نداری، چرا که اگر حتی یک نقطه را بررسی نکنید این احتمال همواره وجود دارد که آن نقطه بر روی چندجمله‌ای نباشد حتی اگر بقیه باشند. اما کاری که می‌توانید کنید، بررسی احتمالاتی این مساله است که بخشی از (برای مثال ۹۰ درصد) تمام نقاط بر روی چندجمله‌ای یکسانی قرار دارند.

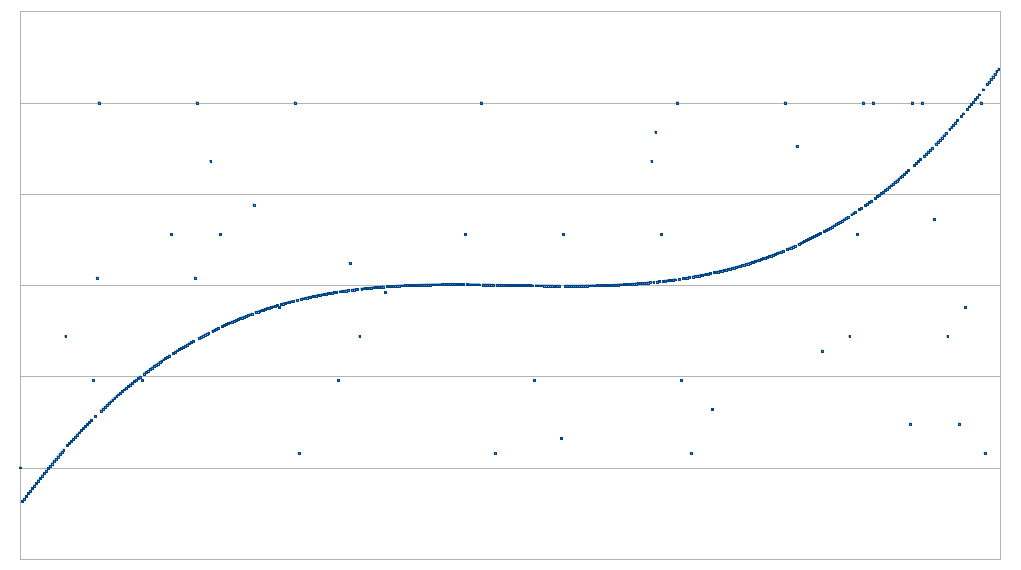
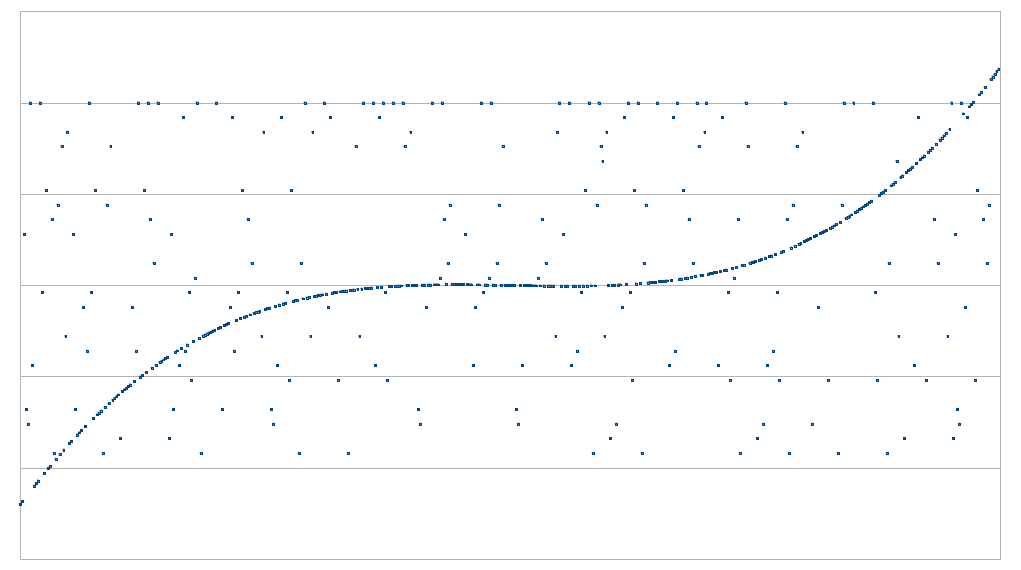
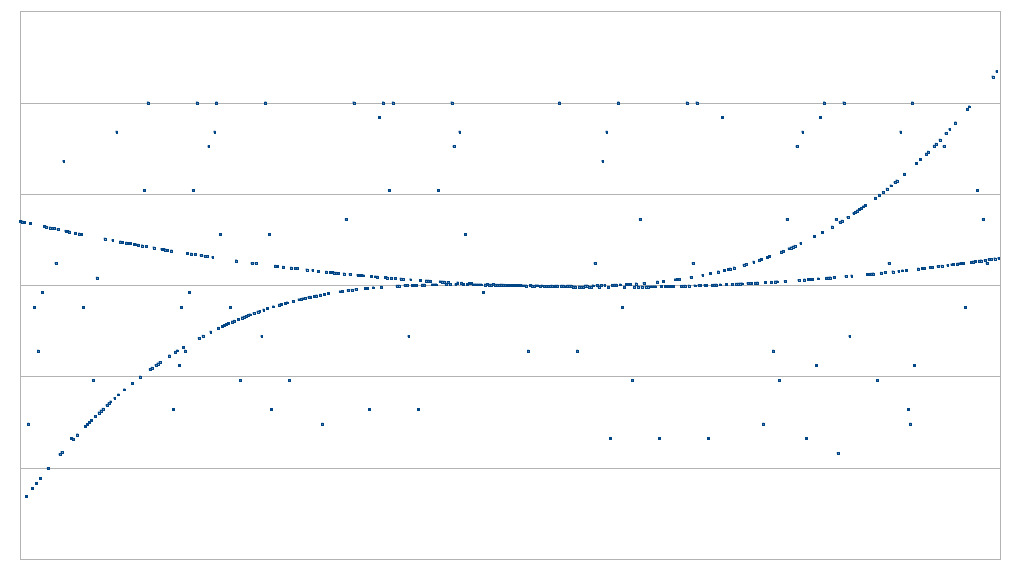
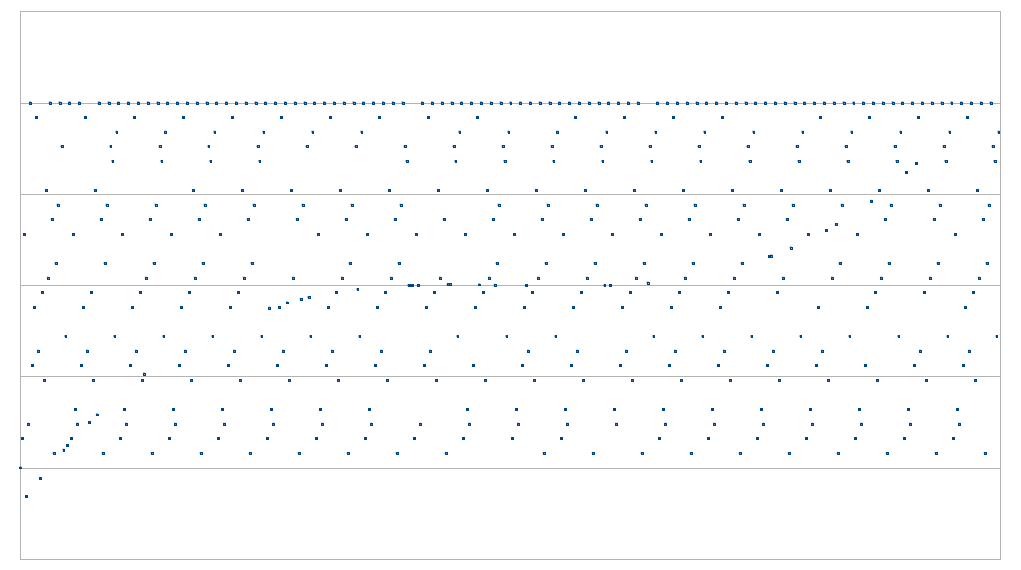
اگر امکان بررسی تمامی نقاط را داشته باشید آن گاه مساله ساده است. اما اگر تنها بتوانید تنها به چند نقطه معدود نگاهی بیاندازید، چه؟ برای مثال اگر بتوانید تقاضای ارائه اطلاعات در خصوص نقطه مشخصی کنید و اثبات‌کننده موظف باشد که در چارچوب قوانین پروتکل، به شما اطلاعات آن نقطه را ارائه کند اما میزان درخواست شما برای نقاط محدود باشد، چه؟ آن‌گاه مساله تبدیل به این می‌شود که به چند نقطه برای بررسی احتیاج دارید تا بتوانید با حد مشخصی از اطمینان، نظر دهید؟

مشخصا بررسی D نقطه کافی نیست. D نقطه دقیقا چیزی است که برای تعریف یک چندجمله‌ای با درجه کمتر از D احتیاج دارید، بنابراین هر مجموعه‌ای از نقاط که دریافت کنید متناظر با یک چندجمله‌ای خواهند بود. اما همان‌طور که در تصاویر بالا مشاهده می‌کنید، D+1 نقطه و بیشتر، اطلاعاتی به ما خواهند داد.

الگوریتم بررسی اینکه آیا مجموعه مشخصی از مقادیر با D+1 جستار بر روی چندجمله‌ای درجه <D هستند یا نه، چندان پیچیده نیست. در ابتدا، زیرمجموعه‌ای تصادفی از میان D نقطه انتخاب می‌کنیم و با استفاده از چیزی مشابه درون‌یابی و تقریب لاگرانژ (برای اطلاعات بیشتر به مقاله پیشین ویتالیک که در میهن بلاکچین ترجمه کردیم، رجوع کنید)، چندجمله‌ای یکتایی که از همه این نقاط می‌گذرد را می‌یابیم. سپس نقطه دیگری که در زیرمجموعه انتخابی نبود را می‌آزماییم تا بررسی کنیم آیا در چندجمله‌ای مذکور قرار دارد یا نه.

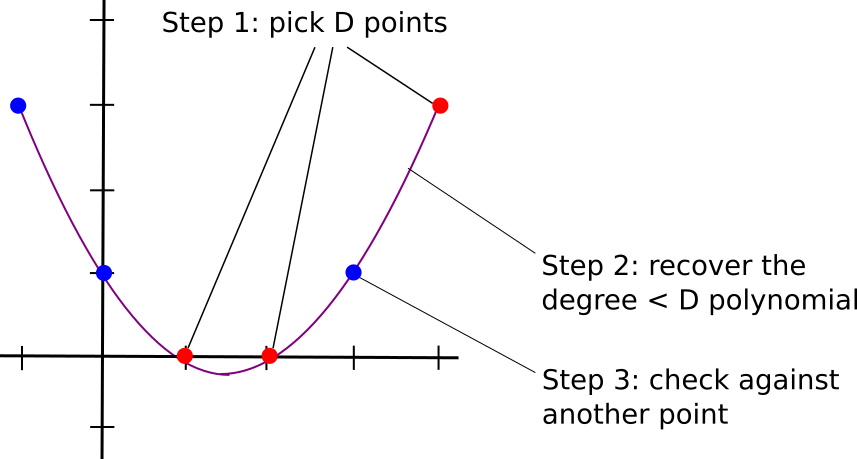
توجه داشته باشید که این روش تنها نوعی تست مجاورت (Proximity Test) است، چرا که همواره این احتمال وجود دارد حتی در صورت قرار داشتن اکثر نقاط بر روی چندجمله‌ای، چند نقطه معدود بر روی آن نباشند و نمونه‌ای شامل D+1 نقطه، شامل آن‌ها نباشد. اما می‌توانیم نتیجه بگیریم که اگر کمتر از ۹۰ درصد نقاط بر روی یک چندجمله‌ای درجه <D باشند، آزمون با احتمال بالایی مردود خواهد شد. به خصوص اگر D+k تفحص انجام دهید و حداقل بخشی (p) از نقاطی که مانند بقیه نقاط بر روی یک چندجمله‌ای نباشند،‌ آن‌گاه احتمال موفقیت در تست برابر خواهد بود با:

(1 - p)^k

اما اگر مشابه مثال‌های مقاله قبلی، مقدار D بسیار بزرگ باشد و بخواهید درجه چندجمله‌ای را با کمتر از D بررسی مشخص کنید چه می‌شود؟ انجام این قضیه البته به شکل مستقیم ناممکن است چرا که هر k<=D نقطه‌ای،‌ حداقل بر روی یک چندجمله‌ای کوچکتر از D درجه یکسان هستند. اما می توان به نحوی و با فراهم آوردن داده‌های کمکی (auxiliary data) این کار را انجام داد و بهره‌وری را به شدت افزایش داد. این دقیقا کاری است که پروتکل‌های پیشین که «گواه مجاورت قابل بررسی احتمالاتی» (PCPP) نام داشتند و یا پروتکل FRI (گواه مجاورت اوراکل تعاملی رید-سالومون سریع) به دنبال تحقق آن است.

نگاهی به مفهوم زیرخطی بودن

برای اثبات ممکن بودن موارد مطرح شده، با پروتکلی به نسبت ساده با مصالحه‌ای ضعیف کار را آغاز می‌کنیم که همچنان قادر به دستیابی به هدف پیچیدگی اثبات زیرخطی خواهد بود. به شکلی ساده‌تر این بدین معنی است که می‌توانید مجاورت به یک چندجمله‌ای با درجه >D را با کمتر از D جستجو ( و کمتر از O(D) محاسبه برای اثبات گواه) ثابت کنید.

ایده کار به شرح زیر است: فرض کنید N نقطه وجود دارد (برای مثال N برابر با یک میلیارد) و همگی بر روی چندجمله‌ای f(x)با درجه کمتر از یک میلیون قرار دارند. چندجمله‌ای دومتغیره پیدا کرده و آن را به فرم g(x, y) نشان می‌دهیم؛ تابعی همچون:

g(x, x^{1000}) = f(x)

این کار را می‌توان به شکل زیر انجام داد: برای عبارت درجه kام در f(x) (برای مثال k=۱۸۵۴۲۳ که منجر به جمله x^۱۸۵۴۲۳*۱۷۴۴ می‌شود)، تابع را به شکل:

x^{k \% 1000} \cdot y^{floor(k / 1000)}

تجزیه می‌کنیم که جواب آن در این مورد مشخص برابر است با:

1744 \cdot x^{423} \cdot y^{185}

با جاگذاری y = x^1000 و به ازای k=۱۸۵۴۲۳، می‌توانید ببینید که جمله بالا دقیقا برابر با:

1744 \cdot x^{185423}

می‌شود.

در گام اول ایجاد گواه، اثبات‌کننده درخت مرکلی از تمام نتایج تابع g(x, y) در تمامی نقاط مربع [ 1 . . . N ] x { x^1000 : 1 ≤ x ≤ N } ایجاد می‌‌کند که برابر است با تمامی یک میلیارد مختصات x برای ستون‌ها و تمامی یک میلیارد مختصات به توان هزار رسیده برای محاسبه مقدار yها که مقادیر ردیف را تشکیل می‌دهند. قطر این مربع برابر است با مقادیر g(x, y) که به فرم g (x, x^1000) است و متناظر با تابع f(x) است.

در گام بعدی اعتبارسنج چندین ستون و ردیف را انتخاب می‌کند (می‌تواند با استفاده از ریشه مرکل، نوعی منبع شبه تصادفی برای انتخاب ایجاد کند تا گواه غیرتعاملی شود) و سپس برای هر ردیف یا ستونی که انتخاب می‌کند، اعتبارسنج درخواست نمونه‌ای (برای مثال شامل ۱۰۱۰ مقدار) از نقاط ردیف یا ستون می‌کند. او اطمینان حاصل می‌کند که یکی از نقاط درخواستی حتما روی قطر باشد. اثبات‌کننده باید در پاسخ، نقاط خواسته شده و شاخه‌های مرکلی که اثبات می کند این اطلاعات، بخشی از داده‌های ابتدایی تحویل داده شده است، را مهیا کند. اعتبارسنج سپس درستی شاخه‌های مرکل را می‌سنجد و بررسی می‌کند که نقاط ارائه شده، واقعا در یک چندجمله‌ای درجه هزار قرار دارند.

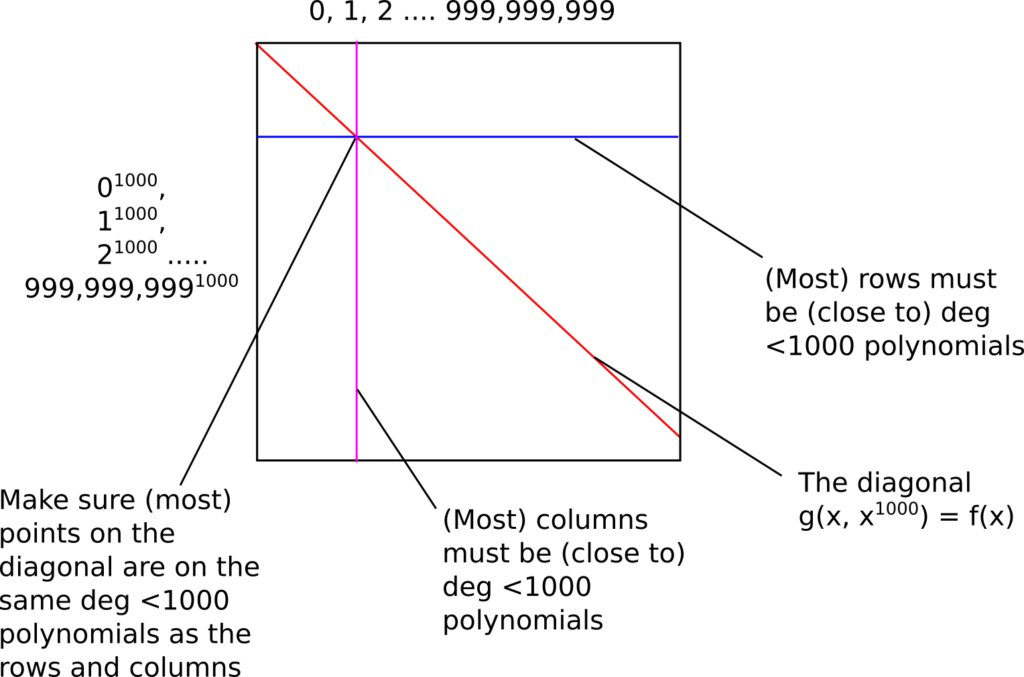
این به اعتبارسنج گواهی آماری می‌دهد که الف) اکثر ردیف‌ها توسط نقاطی پر شده‌اند که بر روی چندجمله‌ای‌هایی با درجه کمتر از هزار هستند. ب) اکثر ستون‌ها از نقاطی تشکیل شده‌اند که که بر روی چندجمله‌ای‌هایی با درجه کمتر از ۱۰۰۰ هستند. پ) خط قطری اغلب بر روی چنین چندجمله‌ای‌هایی است. بنابراین این قضیه اعتبارسنج را متقاعد می‌سازد که اغلب نقاط روی قطر، متناظر با یک چندجمله‌ای با درجه کمتر از یک میلیون هستند.

اگر سی ردیف و سی ستون را انتخاب کنیم، اعتبارسنج باید در مجموع ۱۰۱۰ نقطه*۶۰ (ردیف و ستون) = ۶۰۶۰۰ نقطه را ارائه کند که کمتر از یک میلیون نقطه ابتدایی است اما نه آن قدر کمتر. در خصوص زمان محاسبات، درونیابی چندجمله‌ای‌های با درجه کمتر از هزار نیز هزینه سربار خود را خواهد داشت. گرچه می‌توان با تبدیل درونیابی چندجمله‌ای به زیر درجه دوم (Subquadratic)، کل الگوریتم را همچنان زیرخطی نگه داشت. پیچیدگی برای اثبات‌کننده بیشتر است: اثبات‌کننده باید تمامی چهارضلعی N.N را محاسبه و ارائه کند که در مجموع شامل ۱۰ به توان ۱۸ تلاش محاسباتی است (در واقع کمی بیشتر، چرا که محاسبه و ارزیابی چندجمله‌ای همچنان فوق خطی [superlinear] است). در تمامی این الگوریتم‌ها،‌ اثبات انجام یک محاسبه، به شکلی قابل توجه پیچیده‌تر از انجام آن است: اما همان‌طور که خواهیم دید، سربار محاسباتی می‌تواند این‌قدر بالا نباشد.

میان‌پرده‌ای به نام حساب هم‌نهشتی

پیش از رفتن به سراغ راهکارهای پیچیده‌تر، باید گریزی به دنیای حساب پیمانه‌ای (هم‌نهشتی) – Modular Arithmetic – بزنیم. معمولا وقتی با عبارات جبری و چندجمله‌ای‌ها سر و کار داریم، با اعداد صحیح، به وسیله عملوند/عملگرهایی همچون + – * / (و به توان‌رسانی که در واقع همان ضرب پی‌در‌پی است) کار می‌کنیم و همان نتیجه‌ای را می‌گیریم که از دوران تحصیل آن را آموخته‌ایم: 2 + 2 = 4 و غیره. اما چیزی که ریاضی‌دانان دریافتند این است که این تعریف از جمع، تفریق، ضرب و تقسیم تنها راه ممکن برای تعریف خودمکفی این عملوندها نیست.

ساده‌ترین مثال برای بیان راهی متفاوت برای تعریف این عملگرها، حساب پیمانه‌ای است که این چنین تعریف می‌شود: اپراتور % به معنی «باقی‌مانده را در نظر بگیر» است. همچنین جواب این محاسبه همواره غیرمنفی است. این چنین برای هر عدد اول p می‌توانیم عملیات ریاضی را به شکل زیر بازتعریف کنیم:

x + y >>>> (x + y)%p
x.y >> (x.y)%p
x^y >> (x^y)%p
x - y >> (x - y)%p
x/y >> (x.y^p-2)%p

برای مثال اگر p = 7 باشد، خواهیم داشت:

• ۵ + ۳ = ۱ چرا که باقی‌مانده ۸ تقسیم بر ۷ برابر با ۱ است.
• ۱ – ۳ = ۵ چرا که باقی‌مانده تقسیم ۲- بر ۷ برابر با ۵ است.
• ۲.۵ = ۳
• ۳/۵ = ۲ چرا که ۳ ضرب در ۵ به توان ۵ برابر است با ۹۳۷۵ و باقی‌مانده تقسیم این عدد بر ۷ برابر است با ۲

ویژگی‌های پیچیده‌تری همچون توزیع نیز برقرار است: برای مثال (۲+۴).۳ و ۲.۳ + ۴.۳ هر دو برابرند با ۴. همچنین روابطی همچون اتحاد مزدوج نیز در این فرم جدید حساب برقرار است. تقسیم مشکل‌ترین بخش کار است: نمی‌توانیم از تقسیم عادی استفاده کنیم چرا که می‌خواهیم مقادیر ما همچنان صحیح باقی بمانند و تقسیم عادی عموما جوابی غیرصحیح دارد. توان p – 2 در رابطه تقسیم، نتیجه‌ای از «قضیه کوچک فرما» است که بیان می‌دارد برای هر x غیرصفری که کوچک‌تر از p باشد، رابطه x^p-1 % p = 1 برقرار است.این بدین معنی است که x^p-2 به ما عددی می‌دهد که اگر بار دیگر در x ضرب کنیم، به ما ۱ را نتیجه می‌دهد. بنابراین می‌توانیم بگوییم که x^p-2 (که جواب صحیح دارد) برابر با یک بر روی ایکس است. راه پیچیده‌تر اما سریع‌تر برای محاسبه تقسیم پیمانه‌ای، استفاده از الگوریتم تعمیم‌یافته اقلیدس است که پیاده‌سازی آن به زبان پایتون را می‌توانید از اینجا مشاهده کنید.

به کمک حساب هم‌نهشتی (پیمانه‌ای)، ساختار جدیدی برای حساب ساخته‌ایم و از آن جا که این نوع حساب نیز همچون حساب متداول و سنتی، مشمول تمام روابط آشنایی که می‌شناسیم و از آن استفاده می‌کنیم، می‌شود، می‌توانیم تمامی ساختارها، من‌جمله چندجمله‌ای‌ها را در آن بازسازی کنیم. متخصصین حوزه رمزنگاری عاشق کار کردن با حساب پیمانه‌ای (یا به شکل کلی‌تر میادین متناهی) هستند، چرا که اندازه عدد حاصل از محاسبات در این نوع از حساب محدود است – فارغ از اینکه چه کنید، مقادیر از مجموعه ۰ تا p -1 فراتر نخواهند رفت.

قضیه کوچک فرما نتیجه جالب توجه دیگری نیز دارد. اگر p – 1 مضرب عددی همچون k باشد،‌آن گاه فرمول x –> x^k تصویر (یا برد) کوچکی خواهد داشت. این دین معنی است که تابع تنها می تواند ۱ + کسر (p – 1) بر روی k جواب ممکن داشته باشد. برای مثال اگر x–> x^2 و p = 17 باشد، تنها ۹ جواب ممکن وجود خواهد داشت.

برای توان‌های بیشتر، نتایج حتی بیشتر شوکه‌کننده است. برای مثال اگر k = 8 و p = 17 باشد، آن تابع تنها ۳ جواب دارد. همچنین اگر k = 16 و p = 17 باشد، تنها دو جواب ممکن وجود خواهد داشت. برای x = 0، جواب صفر خواهد بود و برای تمامی اعداد دیگر، جواب ۱ خواهد شد.

حال کمی بهینه‌سازی بیشتر

حال بیایید به نسخه کمی پیچیده‌تر از این سازوکار نگاهی بیاندازیم. در این فرایند سختی کار اثبات‌کننده از ۱۰ به توان ۱۸ تلاش محاسباتی به ۱۰ به توان ۱۵ و سپس ۱۰ به توان ۹ محاسبه کاهش پیدا می‌کند. نخست، به جای محاسبه مجاورت به چندجمله‌ای به کمک اعداد و حساب عادی، آن را با حساب هم‌نهشتی ارزیابی می‌کنیم. همان‌طور که در مقاله پیشین به آن اشاره کردم، اگر نخواهیم جواب محاسبات STARK ما ۲۰۰ هزار رقمی نشود، مجبور به انجام چنین کاری هستیم. در این جا می‌خواهیم به کمک ویژگی تصویر کوچک به توان‌رسانی حساب هم‌نهشتی، پروتکل خود را بهینه‌تر کنیم.

به شکل مشخص با p = 1,000,005,001 کار خواهیم کرد. این عدد به این خاطر انتخاب کردیم: الف) بزرگتر از یک میلیارد است؛ احتیاج داریم که عدد ما بزرگتر از یک میلیارد باشد تا بتوانیم یک میلیارد نقطه را به کمک آن بررسی کنیم. ب) عدد اول است و پ) p – 1 مضرب ۱۰۰۰ است. x^1000 تصویری برابر با 1,000,006 خواهد داشت. این بدین معنی است که تنها 1,000,006  جواب ممکن خواهیم داشت.

نتیجه این خواهد بود که قطر (x, x^1000) حالا فشرده‌تر خواهد بود چرا که تنها تعداد محدودی جواب ممکن داریم. بدین ترتیب تنها به 1,000,006 ردیف احتیاج داریم. بنابراین بررسی کامل g(x, x^1000) حال تنها ۱۰ به توان ۱۵ المان خواهد داشت.

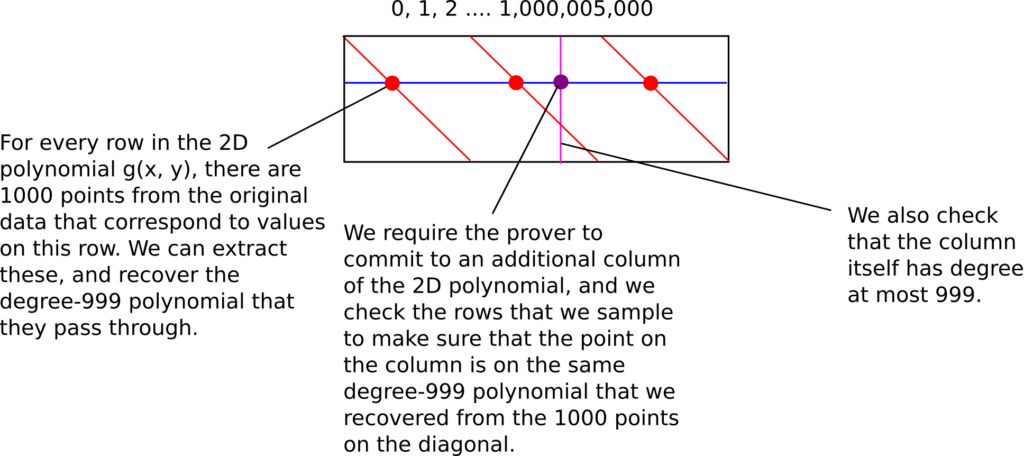
می‌توانیم این کار را یک قدم جلوتر ببریم: می‌توانیم به اثبات‌کننده بگوییم که حاصل g را تنها بر روی یک ستون ارائه کند. نکته در اینجاست که داده اصلی خود شامل ۱۰۰۰ نقطه‌ای که بر روی هر ردیف است می‌شود بنابراین می‌توانیم نمونه‌گیری کنیم و چندجمله‌ای درجه < ۱۰۰۰ متناظری که بر روی آن قرار دارند را پیدا کنیم و سپس بررسی کنیم نقاط متناظر بر روی ستون بر روی همان چندجمله‌ای قرار دارند یا خیر. سپس بررسی خواهیم کرد که ستون خود یک چندجمله‌ای درجه < ۱۰۰۰ باشد.

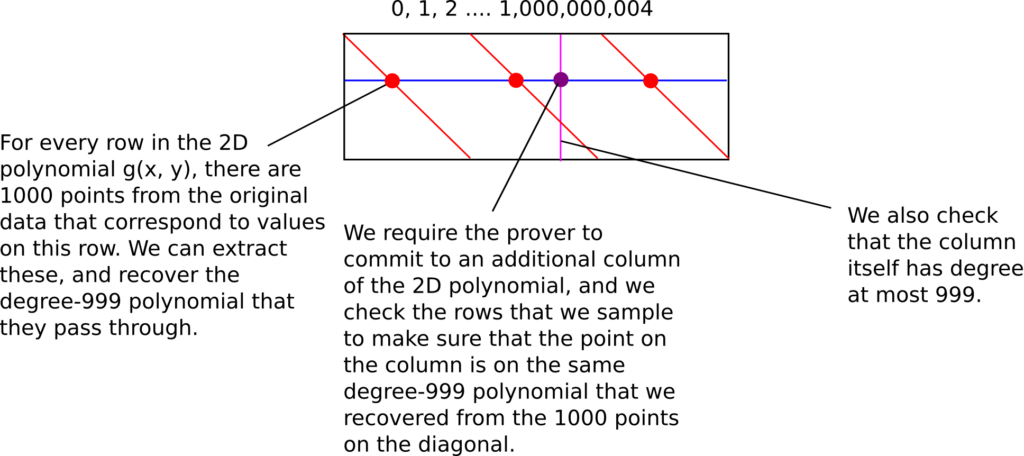
پیچیدگی کار اعتبارسنج همچنان زیرخطی است اما پیچیدگی کار اثبات‌کننده حال به ۱۰ به توان ۹ کاهش یافته است و هم‌اکنون تعداد کوئری‌های آن خطی است (اگر چه در عمل به خاطر سربار محاسبه چندجمله‌ای‌ها، عملیات فوق خطی است).

بهینه‌سازی بیشتر و بیشتر

پیچیدگی اثبات‌کننده هم‌اکنون در کمترین حالت ممکن است اما می توانیم کار اعتبارسنج را ساده‌تر کنیم و از درجه دو به لگاریتمی تقلیل دهیم؛ با بازگشتی کردن الگوریتم. با تمهید بالا کار را آغاز می‌کنیم اما به جای آن که تلاش کنیم چندجمله‌ای را در یک چندجمله‌ای دو بعدی که درجات x و y برابرند بگنجانیم، چندجمله‌ای را در یک چندجمله‌ای دو بعدی که درجه x آن یک عدد ثابت کوچک است، embed می‌کنیم. برای ساده‌سازی، بیایید x را دو بگیریم. بدین ترتیب f(x) را به شکل g(x, x^2) بیان می‌کنیم. این چنین بررسی ردیف‌ها هر بار تنها نیازمند بررسی سه نقطه بر روی هر ردیفی است که از آن نمونه می‌گیریم (دو نقطه بر روی قطر و یکی بر روی ستون).

اگر چندجمله‌ای اصلی درجه‌ای کوچک‌تر از n داشته باشد، حال ردیف‌ها درجه‌ای کمتر از ۲ (ردیف‌ها خط راست هستند) دارند و ستون‌ها درجه‌ای کوچک‌تر از n تقسیم بر ۲. این چنین فرایندی با زمان خطی برای تبدیل مساله اثبات مجاورت به یک چندجمله‌ای درجه < n به مساله اثبات مجاورت به یک چندجمله‌ای با درجه < n تقسیم بر ۲ خواهیم داشت. علاوه بر این، تعداد نقاطی که باید ارائه شود (و متعاقبا پیچیدگی اثبات‌کننده) هر بار با ضریب دو کاهش می‌یابد (الی بن ساسون [Eli Bem-Sasson] مبدع این روش، این جنبه از روش FRI را به تبدیل فوریه سریع تشبیه می‌کند، با این تفاوت که بر خلاف تبدیل فوریه، در هر بازگشت، تنها یک زیر مساله جدید ایجاد می‌شود و نه دو عدد). به همین شیوه، این روش را آن قدر بر روی ستون‌های ایجاد شده در مرحله قبلی ادامه می‌دهیم تا ستون‌ها به قدری کوچک شوند که بتوانیم به راحتی آن‌ها را به شکل مستقیم چک کنیم؛ پیچیدگی نهایی مشابه این سری خواهد بود:

n + \frac{n}{2} + \frac{n}{4} + ... \approx 2n

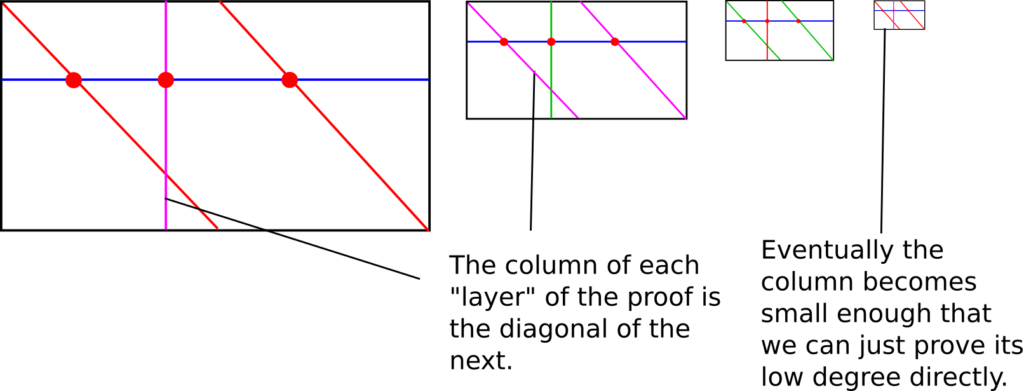
در واقعیت، این فرایند باید چندین دفعه تکرار شود چرا که همچنان احتمال قابل ملاحظه‌ای وجود دارد که یک خرابکار در یک مرحله از فرایند تقلب کند. با این حال، گواه‌های ایجاد شده همچنان چندان بزرگ نیستند. پیچیدگی اعتبارسنجی متناسب با لگاریتم درجه است اما اگر اندازه گواه‌های مرکل را هم در نظر بگیرید با ضریب \log ^{2}n افزایش می‌یابد.

پروتکل FRI واقعی چند تفاوت دارد؛ برای مثال از میدان گالوا دودویی استفاده می‌کند (نوع عجیب و غریب دیگری از میدان متناهی؛ همان چیزی که به عنوان میدان توسیع درجه دوازدهم در این جا درباره‌اش حرف زدم اما با این تفاوت که عدد اول انتخابی ۲ است). همچنین توانی که برای ردیف‌ها استفاده می‌شود نیز عموما ۴ است و نه ۲. این تغییرات به افزایش بهره‌وری کمک می‌کنند و سیستم را برای ساخت استارک‌ها مهیاتر می‌کنند. اما این تغییرات بخش اساسی درک چگونگی کار الگوریتم نیست و اگر واقعا بخواهید، می‌توانید STARK هایی به کمک الگوریتم FRI شرح داده شده در این مطلب بسازید.

صحت روش

واقعیت این است که صحت محاسبات – تعیین احتمال اینکه یک گواه تقلبی به دقت ایجاد شده، پس از تعداد مشخصی آزمون بتواند سیستم را فریب دهد – در این حوزه همچنان فضایی است که نیازمند تحقیق بیشتر است. برای آزمون ساده‌ای که شما ۱۰۰۰۰۰۰ + k نقطه را در نظر می‌گیرید، حد پایینی وجود دارد: اگر مجموعه داده شده دارای این ویژگی باشد که به ازای هر چندجمله‌ای، حداقل بخشی از نقاط (p) این مجموعه بر روی چندجمله‌ای نباشد، آن گاه آزمونی بر روی این دیتاست با احتمال حداکثر (۱ منهای p) به توان k موفق خواهد شد. اما این حد پایین بسیار بدبینانه‌ای است؛ برای مثال ممکن نیست که بتوان بیش از ۵۰٪ به دو چندجمله‌ای درجه پایین به طور همزمان نزدیک بود و احتمال اینکه نخستین نقاطی که انتخاب می‌کنید، همانی باشد که بیشترین نقاط مشترک را دارد، اندک است. برای پروتکل FRI واقعی، پیچیدگی‌هایی در خصوص انواع حملات مختلف ممکن وجود دارد.

بن ساسون اخیرا در مقاله‌ای استواری و صحت FRI را در فرایند کلی STARK بررسی کرده است. خبر خوب این است که برای گذر از آزمون D(x).Z(x) = C(P(x)) که در استارک‌ها صورت می‌گیرد، مقادیر D(x) یک راه‌حل نادرست باید بدترین حالت ممکن باشند؛ آن‌ها باید بیشترین میزان ممکن از هر چندجمله‌ای درستی دور باشند. این مساله به ما می‌گوید که لازم نیست تا آن اندازه مجاورت را چک کنیم. حدود پایین اثبات‌شده کوچک‌تری وجود دارند اما این حدود باعث می‌شوند تا یک استارک به ۱ تا ۳ مگابایت فضا احتیاج داشته باشد: حدود ارائه شده دیگر که اثبات نشده هستند، تعداد بررسی‌های لازم را به یک چهارم کاهش می‌دهند.

در بخش سوم این سری به آخرین چالش ساخت STARKها خواهیم پرداخت: اینکه چگونه می‌توانیم محدودیتی طراحی کنیم که به کمک بررسی چندجمله‌ای‌ها بتوانیم صحت یک محاسبات دلخواه – و نه یک عدد در دنبال فیبوناچی – را ثابت کنیم.

نتیجه‌گیری

در این مطلب ویتالیک بوترین به بررسی جنبه دیگری از گواه‌های اثبات بی‌نیاز به دانش و نوع خاصی از آن به نام ZK-STARK ها پرداخت. در این مقاله بوترین به حساب هم‌نهشتی و نقش آن در بالا برده بهره محاسبات و ساده شدن کار اثبات‌کننده و اعتبارسنج می‌پردازد و به تفاوت پروتکل FRI واقعی با نسخه ساده شده خود می‌پردازد.

شما آینده این نوع از اثبات‌ها را چگونه می‌یابید؟ آیا به زودی محدودیت‌های این روش به قدر کاسته خواهد شد تا بتوانیم همه‌چیز را بی‌نیاز به افشای اطلاعات، به شخص ثالث اثبات کنیم؟