
برای کسانی که به سرمایه گذاری بلند مدت علاقه دارد، احتمالا سود کامپوند (Compound interest) مهمترین مفهومی است که باید بفهمند. هنوز هم بسیاری از سرمایه گذاران طرز کار آن را نمی دانند. و حتی افرادی که قدرت تصاعدی سرمایه گذاریهای کامپوند را درک میکنند، نمیدانند چگونه به طور صحیح تاثیر آن را در محاسبات خود لحاظ کنند. در این مقاله چهار خطای محاسباتی بسیار رایج هنگام برخورد با سود کامپوند و نحوه جلوگیری از آنها را یاد میگیرید.
توضیح مختصر سود کامپوند

اگر با مفهوم سود کامپوند آشنا نیستید، در اینجا نحوه عملکرد آنرا به طور مختصر توضیح میدهیم: اگر ۱۰۰۰ دلار با نرخ ۷ درصد در سال سرمایه گذاری کنید، بعد از یک سال ۷۰ دلار درآمدسود میکنید و سرمایه شما ۱۰۷۰ دلار خواهد بود. اما در سال دوم دیگر ۷۰ دلار درآمد ندارید و به جای آن درآمد شما ۷ درصد از ۱۰۷۰ دلار است که میشود ۷۴.۹۰ دلار. و در سالهای پی در پی درآمد شما بیشتر و بیشتر افزایش خواهد داشت. نمودار زیر نشان میدهد که در صورت ۱۰۰۰ دلار سرمایه گذاری به مدت ۲۵ سال، سرمایه گذاری اولیه چطور رشد می کند.
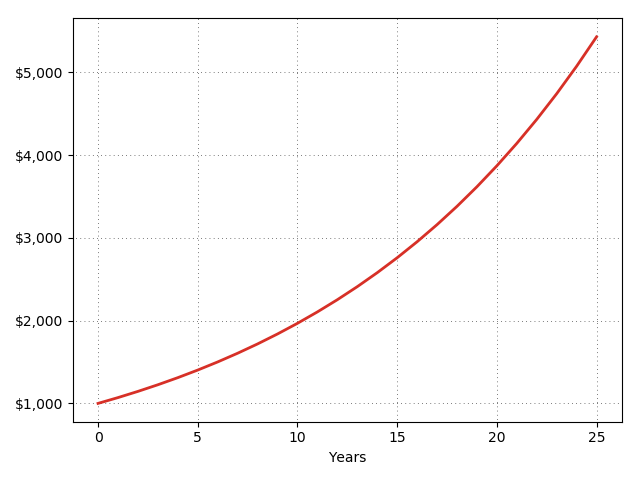
پس از ۲۵ سال، بازده کل سرمایه گذاری شما حدود ۴۴۳ درصد خواهد بود که به طور قابل ملاحظهای بیشتر ۷ ضربدر در ۲۵ سال است (۱۷۵ درصد). به همین دلیل سود کامپوند بسیار قدرتمند است: سرمایه بصورت تصاعدی و نه بصورت خطی رشد میکند.
اشتباهات رایج در محاسبات سود کامپوند
ماهیت تصاعدی محاسبات سود کامپوند پیچیده تر از ریاضی معمولی است که اکثر افراد به صورت روزانه از آن استفاده میکنند و منجر به سوء برداشتهای ریاضی بسیار رایج میشود.
خطای اول: هنگام محاسبه بازده کل در طی چندین دوره
فرض کنید ۱۰۰۰ دلار سرمایه گذاری کردهاید و در سال اول ۱۰ درصد بازده دارید. سپس در سال دوم ۸ درصد دیگر بدست میآورید. درآمد کا شما در دو سال چقدر است؟
بسیاری افراد سریعا میگویند که ۱۰ درصد+ ۸ درصد= ۱۸ درصد، اما محاسبه آن اینقدر ساده نیست.به یاد داشته باشید که بازده ۸ درصدی شما در سال دوم از ۱۰۰۰ دلار اولیه نیست بلکه در عوض از ۱۱۰۰ دلاری است که بعد از سال اول دارید. بنابراین در سال دوم، شما ۰.۰۸ * ۱۱۰۰= ۸۸ دلار بدست میآورید و پس از دو سال در مجموع ۱۱۸۸ دلار کسب میکنید. بدین ترتیب مجموع درآمد شما در دو سال ۱۸.۸ درصد است نه ۱۸ درصد.
جمع و تفریق نرخ تقریبا هرگز روش صحیحی برای انجام محاسبات سود کامپوند نیست. روش صحیح برای محاسبه بازده کل سرمایه گذاری در طی چندین دوره اینگونه است:
R=(1+r1)×(1+r2)×⋯×(1+rn)−1
در فرمول بالا R بازده کل است، n تعداد دوره های متوالی است، و R₁ ، R₂ ، … ، Rₙ نرخ بازده به دست آمده در هر دوره هستند.
یک مثال دیگر: فرض کنید که بعد از چهار سال سرمایه گذاری، به ترتیب ۶، ۱۰، ۷ و ۸ درصد نرخ بازده دریافت کردید. اینگونه کل بازده طی این چهار سال را محاسبه میکنید:
R=1.06×1.10×1.07×1.08−1=0.3474296
بنابراین بازده کل تقریبا ۳۴.۷ درصد است (نه ۳۱ درصد که تنها با جمع کردن آن ۴ رقم بدست میآید).
خطای دوم: هنگام تخمین چگونگی جبران ضرر
این خطا در واقع بسیار شبیه به موارد بالا است. فرض کنید که ارزش بازار پورتفولیوی سرمایه گذاری شما ناگهان ۲۵ درصد افت کرد. چقدر باید بالا برود تا این ضرر بزرگ را جبران کند؟
بسیاری از افراد به سرعت میگویند ۲۵ درصد، اما دوباره چیزها چندان ساده نیست. فقط فرمول قسمت قبل را اعمال کنید و متوجه میشوید که در دو دوره متوالی با نرخ بازده ۲۵- درصد و ۲۵+، بازده کل ۰ درصد نمیشود. درواقع میشود:
(0.75)×(1.25)–1 = –0.0625= –6.25%.
اما نحوه محاسبه جبران ضرر چگونه است؟ میتوانید از فرمول بخش قبلی برای آن استفاده کنید: شما تنها نرخ بازده (منفی) r₁ راداشتهاید و اکنون میخواهید که نرخ بازده r₂ را پیدا کنید و باید برای کل بازده ۰ درصد باید اینکار را بکنید. بنابراین باید معادله زیر را برای r₂ حل کنید:
(1+r1)×(1+r2)−1=0
یا اگر فرمول دقیق را میخواهید، این است:
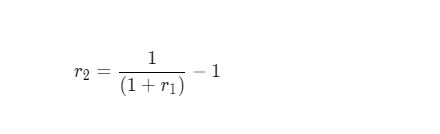
r₁=–۰.۲۵ را جایگزین کنید و r₂ = ۱/۳ بدست میآید. بنابراین جبران ضرر ۲۵ درصد، در واقع باید ۳۳.۳۳ درصد سود کسب کنید.
خطای سوم: هنگام محاسبه میانگین بازده سرمایه گذاری
این خطایی است که حتی سرمایه گذاران باتجربه نیز زیاد مرتکب میشوند. اخیرا ویدیویی در یوتیوب درباره یک دارایی دیدم که طی ۵ سال ۸۳ درصد رشد داشته و یوتیوبر سریع نتیجه گرفت که نرخ رشد آن به طور میانگین سالانه ۱۷ درصد است (احتمالا با تقسیم ۸۳ به ۵ به این عدد رسیده است). البته این عدد درست نیست، دقیقاً مثل اینکه نمیتوانید نرخ رشد برای دورههای متوالی را با یکدیگر جمع کنید. همچینین که محاسبه میانگین حسابی (arithmetic average) آنها نیز منطقی نیست.
روش صحیح این محاسبه بر اساس میانگین هندسی (geometric average) آنها است:
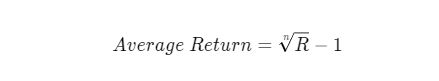
این همان فرمولی است که برای محاسبه به اصطلاح نرخ رشد سالانه کامپوند (یا CAGR) استفاده می شود که اصطلاحی است که به طور گسترده در دنیای سرمایه گذاری استفاده می شود.(تنها تفاوت این است که هنگام محاسبه CAGR، یک دوره لزوما یک سال است.)
اگر آن فرمول را در همان دارایی که در ۵ سال ۸۳ درصد رشد کرده است اعمال کنید، متوجه میشوید که میانگین بازده سالانه آن تقریباً ۱۲.۸۵ درصد است که به طور قابل توجهی کمتر از ۱۷ درصد ذکر شده توسط یوتیوبر بوده اما هنوز هم نرخ رشد فوقالعادهای است.
یکی دیگر از کاربردهای بسیار رایج فرمول بالا، تبدیل نرخ سالانه به نرخ ماهانه است. به عنوان مثال میتوانید برای محاسبه نرخ ۶ درصد در سال استفاده کنید که میشود ۰.۴۸۶ درصد در ماه؛ این نرخ کمی کمر از ۰.۵ درصد است که با تقسیم نرخ سالانه به ۱۲ بدست میآید.
توجه داشته باشید که می توان به راحتی ریشه یک مبنای n را در هر ماشین حساب با عملگر تصاعدی (که معمولاً توسط ^ ، xⁿ یا برخی نمادهای مشابه نشان داده میشود) محاسبه کرد. برای اینکار میتوان از ویژگی نیز استفاده کرد:
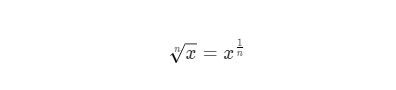
به عنوان مثال برای محاسبه معادل ماهانه ۶ درصد در سال، باید ۱.۰۶^(۱/۱۲)–۱ را در ماشین حساب بزنید.
خطای چهارم: هنگام درنظر گرفتن تورم
از ژانویه ۲۰۰۰ تا ژانویه سال ۲۰۲۰، نرخ بازده اسمی (nominal return rate) شاخص S&P 500 با توجه به سرمایه گذاری مجدد همه سودهای دریافتی، ۲۲۱ درصد بود(منبع: Moneychimp). با این حال در همین دوره ، تورم انباشته (cumulative inflation) در ایالات متحده تقریباً ۵۳ درصد بود (منبع: BLS). با در نظر گرفتن این اعداد، آیا میتوانید بازده واقعی شاخص S&P 500 را در این ۲۰ سال که برای تورم تعدیل شده، محاسبه کنید؟
متأسفانه پاسخ ۱۶۸ درصدی شما با کم کردن ۵۳ از ۲۲۱ درصد صحیح نیست. پاسخ صحیح ۱۱۰ درصد است، نرخی که بطور قابل ملاحظهای کمتر است.
به همان روشی که براس محاسبه سود کامپوند باید از ضربها به جای جمع استفاده کنید، باید تفریق را جایگزین تقسیم کنید. اینگونه میتوانید نرخ بازده واقعی یک سرمایه گذاری معین که برای تورم تنظیم شده را محاسبه کنید:
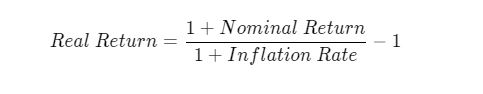
صحبت پایانی
در واقع محاسبات مربوط به سود کامپوند پیچیده تر از ریاضی معمولی است که روزمره استفاده میکنیم. با این حال واقعا علم ساخت موشک نیست و اکنون که از این خطاهای رایج آگاه هستید، بعید است که دوباره آنها را مرتکب شوید. اگر شک داشتید، به فرمولهای موجود در این مقاله مراجعه کرده و محاسبات خود را دوباره چک کنید.



